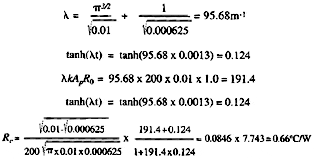Accident? Consider the scenario where a designer wishes to incorporate a newly developed device into a system and soon learns that a heat sink is needed to cool the device. The designer finds a rather large heat sink in a catalog which marginally satisfies the required thermal criteria. Due to other considerations, such as fan noise and cost constraints, an attempt to use a smaller heat sink proved futile, and so the larger heat sink was accepted into the design. A prototype was made which, unfortunately, burned-out during the initial validation test, the product missed the narrow introduction time, and the project was canceled. What went wrong?
The reasons could have been multi-fold. But, under this scenario, the main culprit could have been the spreading resistance that was overlooked during the design process. It is very important for heat sink users to realize that, unless the heat sink is custom developed for a specific application, thermal performance values provided in vendor’s catalogs rarely account for the additional resistances coming from the size and location considerations of a heat source. It is understandable that the vendors themselves could not possibly know what kind of devices the users will be cooling with their products.
Introduction
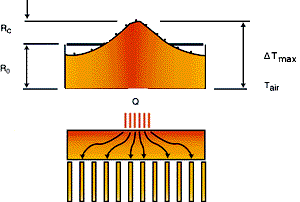
Spreading or constriction resistances exist whenever heat flows from one region to another in different cross sectional area. In the case of heat sink applications, the spreading resistance occurs in the base-plate when a heat source of a smaller footprin footprint area is mounted on a heat sink with a larger base-plate area. This results in a higher local temperature at the location where the heat source is placed. Figure 1 illustrates how the surface temperature of a heat sink base-plate would respond as the size of the heat source is progressively reduced from left to right with all other conditions unchanged: the smaller the heat source, the more spreading has to take place, resulting in a greater temperature rise at the center. In this example, the effect of the edge surfaces of the heat sink is ignored and the heat source is assumed to be generating uniform heat flux.
In cases where the footprint of a heat sink need not be much larger than the size of the heat source, the contribution of the spreading resistance to the overall device temperature rise may be insignificant and usually falls within the design margin. However, in an attempt to remove more heat from today’s high performance devices, a larger heat sink is often used and, consequently, the impact of spreading resistance on the performance of a heat sink is becoming an important factor that must not be ignored in the design process. It is not uncommon to find in many high performance, high power applications that more than half the total temperature rise of a heat sink is attributed to the spreading resistance in the base-plate.
The objectives of this article are:
1) to understand the physics and parameters associated with spreading resistance
2) to provide a simple design correlation for accurate prediction of the resistance
3) to discuss and clarify the concept of spreading resistance with an emphasis on the practical use of the correlation in heat sink applications
The correlation provided herein was originally developed in references 1 and 2. This article is an extension of the earlier presentation.
Spreading Resistance
Before we proceed with the analysis, let us attend to what the temperature distributions shown in Fig. 1 are telling us. The first obvious one, as noted earlier, is that the maximum temperature at the center increases as the heat source becomes smaller. Another important observation is that, as the temperature rises in the center, the temperatures along the edges of the heat sink decrease simultaneously. It can be shown that this happens in such a way that the area-averaged surface temperature of the heat sink base-plate has remained the same. In other words, the average heat sink thermal performance is independent of the size of a heat source. In fact, as will be seen later, it is also independent of the location of the heat source.
The spreading resistance can be determined from the following set of parameters:
- footprint or contact area of the heat source, As
- footprint area of the heat sink base-plate, Ap
- thickness of the heat sink base-plate, t
- thermal conductivity of the heat sink base-plate, k
- average heat sink thermal resistance, R0
We will assume, for the time being, that the heat source is centrally mounted on the base-plate, and the heat sink is cooled uniformly over the exposed finned surface. These two assumptions will be examined in further detail. Figure 2 shows a two-dimensional side view of the heat sink with heat-flow lines schematically drawn in the base-plate whose thickness is greatly exaggerated. At the top, the corresponding surface temperature variation across the center line of the base-plate is shown by the solid line. The dotted line represents the average temperature of the surface which is, again, independent of the heat source size and can be easily determined by multiplying R0 with the total amount of heat dissipation, denoted as Q.
As indicated in Fig. 2, the maximum constriction resistance Rc, which accounts for the local temperature rise over the average surface temperature, is the only additional quantity that is needed for determining the maximum heat sink temperature. It can be accurately determined from the following correlation.
Figure 2 – Two dimensional schematic view of local resistance or temperature variation of a heat sink shown with heat flow Lines
Note that the correlation addresses neither the shape of the heat source nor that of the heat sink base-plate. It was found in the earlier study that this correlation typically results in an accuracy of approximately 5% over a wide range of applications with many combinations of different source/sink shapes, provided that the aspect ratio of the shapes involved does not exceed 2.5. See references 1 and 2 for further discussions.
Example Problem
Consider an aluminum heat sink (k = 200W/mK) with base-plate dimensions of 100 x 100 x 1.3 mm thick. According to the catalog, the thermal resistance of this heat sink under a given set of conditions is 1.0 °C/W. Find the maximum resistance of the heat sink if used to cool a 25 x 25 mm device.
Solutions
With no other specific descriptions, it is assumed that the heat source is centrally mounted, and the given thermal resistance of 1.0 °C/W represents the average heat sink performance. From the problem statement, we summarize:
- As = 0.025 x 0.025 = 0.000625 m2
- Ap = 0.1 x 0.1 = 0.01 m2
- t = 0.0013 m
- k = 200 W/mK
- R0 = 1.0 °C/W
Therefore,
Hence, the maximum resistance, Rtotal , is:
Rtotal = Ro + Rc = 1.0 + 0.66 = 1.66 °C/W
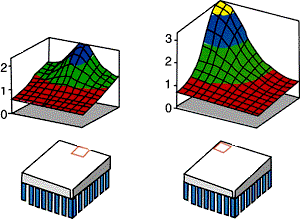
Readers should note the far right temperature distribution in Fig. 1 which is the result of a numerical simulation for the present problem in rectangular coordinates.
Effect of Source Location
In the following two sections, we will limit our examination to the current example problem. As we shall see, the result of this limited case study will allow us to draw some general yet useful conclusions. Suppose the same heat source in the above example was not centrally located, but mounted a distance away from the center. Obviously, the maximum temperature would further rise as compared to that found in the above example. Figure 3 shows the local resistances corresponding to two such cases:
Figure 3 – Heat-sink local resistance showing the effect of source location:
from L to R, heat source at (37.5,0) and (37.5,37.5)the first one is for the case where the heat source is mounted midway along the edge, and the other, where it is mounted on one corner of the heat sink. For these two special cases, the maximum spreading resistance can be calculated by using Eq. (1) for Rc with input parameters t and R0 modified as shown below:
| Rc = C x Rc (Ap,As,k,t/C,R0/C) | (3) |
with for the first case, and C = 2 for the second case. It is to be noted that this expression is independent of the source size. Numerically, for the current problem with a 25 x 25 mm heat source, it results in the maximum spreading resistances of 1.29 and 2.38 °C/W, or the total resistances of 2.29 and 3.38 °C/W for the first and second cases, respectively. For both cases, it can be shown that the average surface resistance has not changed from unity.
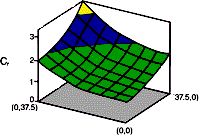
For other intermediate source locations, numerical simulations were carried out and a plot is provided in Fig. 4 for the correction factor Cf which can be used to compute the total resistance as
| Rtotal = R0 + Cf Rc | (4) |
where Rc is determined from Eq. (1), given for the case with the heat source placed at the center.
Figure 4 – Correction factor as a function of source locationThe coordinates in Fig. 4 indicate the location of the center of the heat source measured from the center of the base-plate in mm: the case with a centrally located heat source corresponds to (0,0), and the cases shown in Fig. 3 correspond to (37.5,0) and (37.5,37.5) for the first and second cases, respectively. Only one quadrant is shown in Fig. 4 as they would be, owing to the assumption of uniform cooling, symmetrical about (0,0). As can be seen from the figure, the correction factor increases from 1 as the heat source is placed away from the center. It is worthwhile noting that the increase is, however, very minimal over a wide region near the center, and most increases occur closer to the edges.
Unlike C in the earlier expression, Cf is case dependent (i.e. it depends on the heat-source size). However, it was found that the plots of Cf obtained for many other cases exhibit essentially the same profile as that shown in Fig. 4, with magnitudes at the corners determined from Eq. (3), and the domain of the plot defined by the maximum displacement of the heat source. Based on this observation, a general conclusion can be made: for all practical purposes, as long as the heat source is placed closer to the center than to the edges of the heat sink, the correctional increase in the spreading resistance may be ignored, and Cf =1 may be used. As noted above, this would introduce a small error of no greater than 5-10% in the spreading resistance which, in turn, is a fraction of the total resistance.
So far, we have assumed a uniform cooling over the entire finned-surface area of the base-plate. Although this is a useful assumption, it is seldom realized in actual situations. It is well known that, due to the thinner boundary layer and the less down-stream heating effect, a device would be cooled more effectively if it is mounted toward the air inlet side. Again, a numerical simulation is carried out using our example problem with the boundary layer effect included.
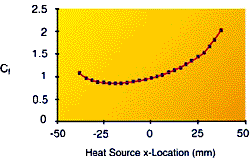
Figure 5 shows the resulting modified correction factor as a function of the distance from the center of the heat sink to the heat source placed along the center line at y=0: x = -37.5 mm corresponds to the front most leading edge location of the heat source and x = 37.5 mm the rear most trailing edge placement.
Figure 5 – Correction factor modified for boundary layer effect at y=0As can be seen from the figure, it is possible to realize a small improvement by placing the heat source forward of the center location where Cf < 1. However, it was experienced in practice that accommodating a heat source away from the center and ensuring its mounting orientation often cause additional problems during manufacturing and assembly processes.
Summary and Discussion
A simple correlation equation is presented for determining spreading resistances in heat sink applications. A sample calculation is carried out for a case with a heat source placed at the center of the heat sink base-plate and a means to estimate the correction factor to account for the effect of changing the heat-source location is provided. It is to be noted that the correlation provided herein is a general solution which reduces to the well known Kennedy’s solution3 when R0 approaches 0: the mathematical equivalent of isothermal boundary condition. Kennedy’s solution is valid only when R0 is sufficiently small such that the fin-side of the heat sink base-plate is close to isothermal. Otherwise, Kennedy’s solution, representing the lower boundary of the spreading resistance, may result in gross underestimation of the resistance.
The earlier study revealed that, depending on the relative magnitude of the average heat sink resistance, the spreading resistance may either increase or decrease with the base-plate thickness. If the heat sink resistance is sufficiently small, as in liquid cooled heat sink applications, the spreading resistance always increases with the thickness, and an optimum thickness does not exist. On the other hand, if the heat sink resistance is large, as experienced in most air-cooled applications, the spreading resistance decreases with the thickness and a finite optimum thickness exists.
It is to be noted that the present correlation calculates the spreading resistance only in the base-plate and does not account for the effect of additional spreading that may exist in other places, such as the fins in a planar heat sink. This additional spreading in the fins usually affects the spreading resistance in a similar way to a thicker base-plate. The current author found that an increase of 20% in the base-plate thickness during the calculation roughly accounts for the effect of this additional spreading in the fins of the same material for most planar heat sinks under air cooling. No modification is required for pin-fin heat sinks.
References
| 1. | S. Lee, S. Song, V. Au, and K.P. Moran, Constriction/Spreading Resistance Model for Electronic Packaging, Proceedings of the 4th ASME/JSME Thermal Engineering Joint Conference, Vol. 4, 1995, pp. 199-206. |
| 2. | S. Song, S. Lee, and V. Au, Closed Form Equation for Thermal Constriction/Spreading Resistances with Variable Resistance Boundary Condition, Proceedings of the 1994 IEPS Conference, 1994, pp. 111-121. |
| 3. | D. P. Kennedy, Spreading Resistance in Cylindrical Semiconductor Devices, Journal of Applied Physics, Vol. 31, 1960, pp. 1490-1497. |