In the current world of heat transfer analysis, most work is performed with numerical simulation. However, there are analysis methods, which are faster and useful for early estimates or even design guidance, that are beneficial to thermal engineers. A recent ECM article [1] mentioned the concept of the critical radius when discussing the cooling/insulating effect of wire insulation; this is one of those useful analysis methods that thermal engineers should know about. Critical radius is rarely discussed today and many of the standard heat transfer texts do not mention it, even in passing.
This author’s modest heat transfer library contains no books with references to the critical radius concept – even the thorough Heat Transfer Handbook from Wiley does not mention critical radius in its voluminous 1,500 pages. The author was taught this concept in his undergraduate heat transfer class at Georgia Tech and this article is a similar introduction to the subject, derived from the class notes [2].
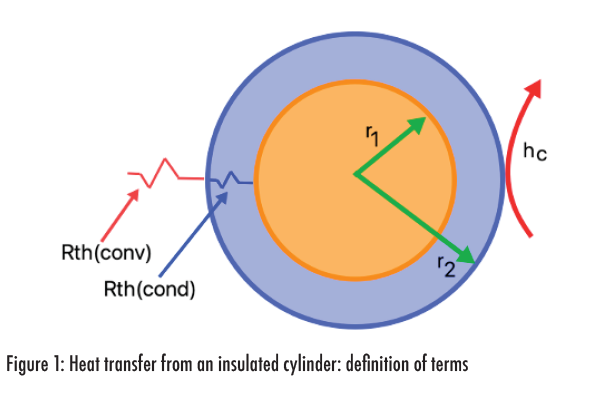
Figure 1 shows the basics of the cylindrical heat transfer case in cross section. While this is often used to examine wire insulation diameters and how to reduce wire temperatures from resistive heating, the concept applies to any similar object with two materials at different distances from the center (not only cylindrical but also spherical), and some method of heat transfer from the outer surface. In theory, other shapes can also be developed but the concept of the critical radius is the one found in older literature with circular cross sections.
In this article, the inner region with radius r1 is the heat generating section. The outer region between r1 and r2 is the added, or outer, layer. Heat transfer from the outer layer is a convection loss with a convective coefficient of hc. Note that different correlations could be used for the coefficient: for wiring, natural convection is most common, but in some environments, such as with fans moving air, a forced air convection coefficient might be appropriate. Radiation may also be included if the temperature difference from r2 to ambient is significant. The two thermal resistances of conduction through the outer region and convection from the outer surface are represented by Rth(cond) and Rth(conv) respectively.
Before writing the equations and finding the analytical solution, the reader should note that changing r1 and r2 influences the thermal resistances in opposite directions. Holding r1 constant for a moment, as r2 increases the value of Rth(cond) increases as the heat must conduct a longer distance through more material. However, as r2 increases, the surface area of the outer region for convective heat dissipation also increases, which reduces Rth(conv). When these two resistances move in opposite directions, it becomes one of the maximum/minimum problems (optimization) seen in calculus courses.
Changing r1’s value and holding r2 constant produces a different observation. As r1 approaches r2, the conductive thermal resistance of the outer layer shrinks and the heat transfer at the r2 boundary remains the same. This means the heat transfer is maximized. However, in critical radius problems, r1 is usually fixed, so this situation is not typically encountered. Thus, r1 is normally considered fixed in these problems because wire size or other cylindrical heat source size is fixed.
Detailing the variable r2 situation in equations, results in the following: Rt heat transfer resistance is the sum of the two parts shown in equation 1, namely
and when the thermal resistances are inserted in terms of the one-dimensional heat transfer equations, this becomes equation 2:
where k2 is the thermal conductivity of the outer region. The terms L and A2 describe this as a 3D problem where a cylinder of length L is in view and A2 is the outer area of the cylinder at r2. This third dimension will cancel out shortly in the derivation of the critical radius. Further, this equation shows the total thermal resistance is also a function of the thermal conductivity k2. The entire thermal path depends on the thickness of the outer region, its thermal conductivity, and the heat transfer coefficient from the r2 surface.
The optimization problem can now be created and solved. First, we need to meet the condition (equation 3)
where q is the applied power. For the critical radius, the optimization is a maximum heat flow rate or a minimum total thermal resistance for the geometry parameter r2. Using the equation for total thermal resistance, the expression for q (equation 4) is
where t1 is the internal cylinder temperature (at r1) and tamb is the ambient temperature. Inserting equation 4 into the equation 3 condition results in:
Solving this for r2, we find the critical radius to be (equation 6):
Thus, the ratio of the outer layer’s thermal conductivity to the outer surface’s heat transfer coefficient determines the critical radius, at which the heat flow is a maximum in the system. If the system’s outer radius is already larger than the critical radius, then any added thickness will impede heat transfer and increase the inner section’s temperature.
This result is for a cylindrical system, but it is also possible to generalize this to add a planer and spherical system shown in equation 7:
where n=1 for a planer wall (i.e., no critical radius but only added insulation)
n=2 for a cylinder
n=3 for a sphere (derived similarly to cylindrical case)
This formula is helpful for quickly evaluating any cylindrical or spherical system for the thermal impact of changes in radii, changes in thermal conductivity, or changes due to a different heat transfer method (changing hc). These allow an engineer to quickly assess a possible design change, when tuning a design, without resorting to a longer FEA/CFD analysis.
Where can this be applied? Wire and wire insulation is one area where this can help. A larger wire insulation diameter might be helpful to remove Joule heating in the wires. Other applications can be found on PCBs with conformal coatings applied. Large flat integrated circuits will likely have added thermal resistance since they are planer when compared to their heights. However discrete cylindrical components, such as electrolytic capacitors, can remove heat more effectively with a conformal coating. This is advantageous if these are in a power supply and see higher duty cycles and temperatures. This is counterintuitive for many people but, by demonstrating this with the equations developed here (and shown by testing), the thermal design of a system can be enhanced.
The author is grateful to the late Dr. S. Peter Kezios who taught this and other heat transfer concepts in his Transport Phenomena I class at Georgia Tech in 1980. Dr. Kezios was also a past president of the ASME in the late 1970s. This article is dedicated to him for his work teaching future engineers about sound fundamentals, and for which I am thankful.
References
[1] Wilcoxon, R., Effect of Thermocouple Size, Electronics Cooling Magazine, Spring 2024, pp. 9-11
[2] Kezios, S. Peter, Transport Phenomena I, School of Mechanical Engineering, Georgia Institute of Technology, Atlanta GA, 1979 (class notes, published by Georgia Tech)