In several earlier issues of Electronics Cooling, I discussed the thermal conductivity of air as a function of temperature and pressure. Therein, it was stated that the temperature dependence cannot be neglected, but that the pressure dependence, under ‘normal’ conditions, is virtually absent.
But what is ‘normal’ these days? In ‘normal’ electronic systems we, indeed, need pressures well below 1 Pa (10-5 bar) to see any significant deviation. However, there is another parameter, which is directly involved in the physics that describe the pressure-dependence; namely, length. More precisely, the mean free path that determines the average length between a collision of two particles (i.e., electrons, atoms, molecules).
Reducing the pressure reduces the number of particles and increases this length scale. Reducing the relevant dimensions of the system (such as the distance between two parallel plates) does not affect this length scale, except when they become smaller than the mean free path. At room temperature, the molecular mean free paths for nitrogen, argon and neon are, respectively, 65, 300 and 880 nm. Obviously, when we talk about microchannels, MEMS and nanostructures, we surely enter the domain that is ruled by the mean free path.
The ratio between the mean free path and a characteristic dimension (e.g., the distance between two infinite plates) is called the Knudsen number: Kn. This number is very important for the characterization of gaseous flows in the micro- and nanoregime. This note discusses only the influence on the thermal conductivity. It appears that increasing Kn beyond 1 is a very efficient way of reducing the thermal conductivity, theoretically by orders of magnitude, thereby opening new grounds for very efficient thermal insulation and thermoelectricity. Physically, the theory is by no means trivial, but an approximate formulation that might be helpful to designers is presented below.
Ke/K0 = 1/(1+C/PP) (1)
in which:
| Ke/K0 | thermal conductivity ratio | |
| C | constant equal to 7.6*10-5 | [mK/N] |
| PP | pressure parameter, P*d/T | [N/mK] |
| Ke | thermal conductivity at reduced pressure |
[W/mK] |
| K0 | thermal conductivity at 1 bar | [W/mK] |
| P | pressure | [Pa] |
| d | plate distance | [m] |
| T | absolute temperature | [K] |
While this formula essentially describes Low Pressure Theory only (the so-called Slip Flow Theory) and should be replaced by the Free Molecule Theory when the pressure parameter falls below 10-4, the formula gives remarkably good results for much lower values. The formula is shown graphically in Figure 1.
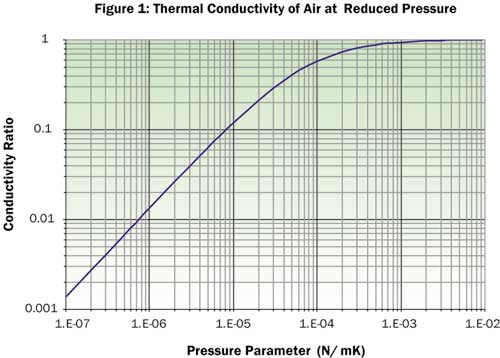 |
Practical Examples
- 1. Take T=300 K, and d=1 cm. To get a tenfold reduction in thermal conductivity, the pressure parameter should be about 10-5. This means that the pressure should be below 0.3 Pa.
- What should the distance be to achieve the same reduction at normal pressure? The distance should be less than 3 x 10-8 m, or 30 nm.
Source: Fluid Flow Databook, General Electric, Genium Publishing, Section 410.2, May 1982.






