Simple Formulas for Estimating Thermal Spreading Resistance

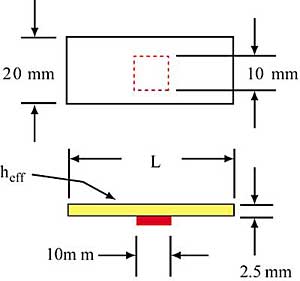
A problem commonly encountered in the thermal analysis of electronic packages is that of thermal spreading resistance. Thermal spreading resistance occurs as heat flows by conduction between a source and a sink with different cross-sectional areas. Examples of two situations involving spreading heat flow are shown in Figure 1. One example is that of a chip mounted on the bottom surface of a substrate. Another is that of a module package with a thermal grease path between a chip and the module cap. In either case heat flows from the chip across an area A₁ into the substrate or cap and spreads out to leave across an area A₂.

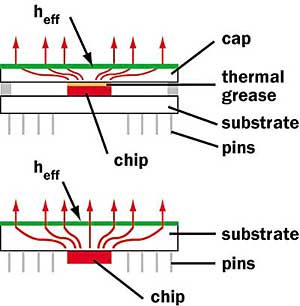Figure 1. Example of spreading heat flow in two types electronic packages.Exact analytic solutions to the partial differential equations governing thermal spreading for situations similar to that described above have been reported in the literature [1,2]. These solutions address the general problem of determining the temperatures throughout multi-layer plates with multiple heat sources located on one side of a multi-layer structure with a uniform heat transfer coefficient applied to the opposite side. For the purposes of this article we will restrict our attention to a single square plate or thermal spreader with a centrally located square heat source on one side and a heat transfer coefficient applied to the opposite side. If we can determine the temperature, T_max, at the center of the heat input area on the plate for a given heat transfer rate (i.e., power dissipation), q, and reference temperature, T_ref, we can determine the total thermal resistance and its components (i.e., conduction and convection). The total thermal resistance from T_max to T_ref is simply:

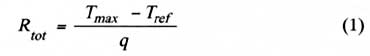The total thermal resistance is composed of a conduction/spreading resistance and a convection resistance. The conduction/spreading resistance, R_sp, includes spreading effects and is influenced by the effective heat transfer coefficient acting on the surface. The convective thermal resistance, R_conv , is given by:

where A_s is the surface area of the plate or thermal spreader and h_eff is the effective heat transfer coefficient acting on the surface. The total thermal resistance from T_max to T_ref is given by:

Unfortunately, even for the restricted case under consideration here, the solution to find T_max is a complicated infinite series with equally complicated coefficient terms. Automating the solution for calculation requires a considerable amount of programming and is not readily amenable to incorporation in spreadsheets, such as Microsoft Excel.

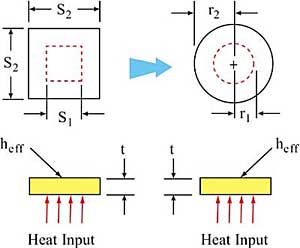Figure 2. Transformation of square into circular geometry.Fortunately, Lee et al. [3] developed a closed form solution that can provide results very close to the exact solution and is easily amenable to incorporation in a spreadsheet or similar calculation scheme. The solution is based upon a circular plate with a circular heating area, so our square geometry must be first transformed into a circular geometry as illustrated in Figure 2. The transformation is based upon the areas of the plate and heat source being the same in both the square and circular geometries. So, the equivalent radii in the circular case are given by:

The equivalent radii, r₁ and r₂, may be then used along with the thermal conductivity, k, of the spreader plate with thickness, t, in the following equations:

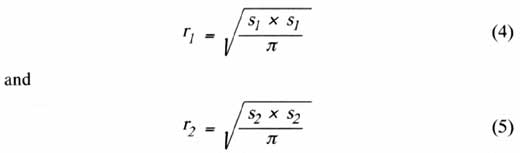
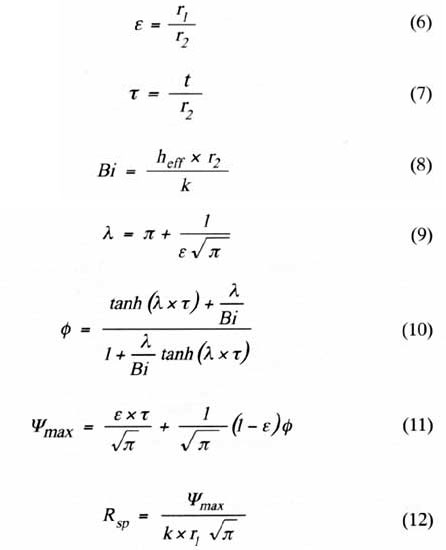Equation (12) gives the thermal conduction spreading resistance from T_max to the convective surface.

To demonstrate the accuracy of these formulas, calculations were performed and compared with results obtained from the exact series solution using TAMS (Thermal Analyzer for Multilayer Structures) [1]. These calculations were based upon a fixed heat input area of 10 x 10 mm on a square thermal spreader plate 2.5 mm thick and ranging in size from 20 x 20mm to 40 x 40 mm. Two values of thermal conductivity were used, ranging from 25 W/m�K for a material such as alumina to 400 W/m�K for a material such as copper. Similarly, two values of heat transfer coefficient were used ranging from 250 W/m²�K representing that achievable with a lower performance forced convection heat sink to 1000 W/m²�K representing that achievable with a high performance forced convection heat sink.

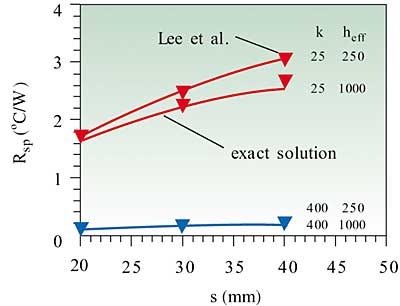
A comparison of the results for the total thermal resistance, R_tot, versus plate size using the spreading formulas of Lee et al. and the exact solution are shown in Figure 3. As may be seen in the figure, there is no discernable difference between the two sets of results. Based upon the calculated values the percent error for the simplified formulas is between -1.2 % to +3.9 % over the full range of parameters considered. A similar comparison is shown in Figure 4 for the conduction/spreading thermal resistance, R_sp, versus plate size. Although there is a small difference in results for k = 25 and h_eff = 1000 the comparison is still very good. Based upon the calculated values the percent error for the simplified formulas in this case is between -2.1 % to +4.8 % over the full range of parameters.

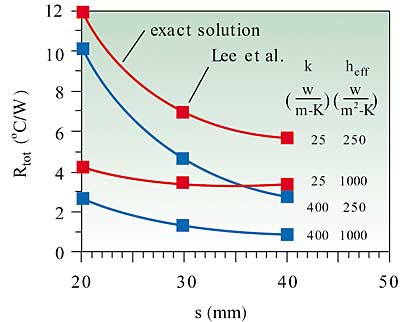Figure 3. Results for R_tot using Lee et al. formulas and exact solution.
Figure 4. Results for Rsp using Lee et al. formulas and exact solution.
Figure 5. Non-square thermal spreader plate geometry.Calculations were also performed to assess the accuracy of the simplified formulas when applied to a non-square thermal spreader plate. The geometry considered is shown in Figure 5. In this case the value of r₂ to use in equations (6) and (7) is given by:

where W is the width of the spreader plate and L is the length of the plate. The plate length considered was varied from 20 to 50 mm. A plate thermal conductivity of 25 W/m�K and a heat transfer coefficient of 250 W/m²�K were used for these calculations. The results obtained for R_tot (i.e. conduction/spreading and convection) and R_sp (conduction and spreading) are shown in Figure 6. The percent error in R_tot between the exact solution and the simplified formulas is shown in Figure 7. As may be seen in the figure the percent error is progressively greater as the plate length increases.

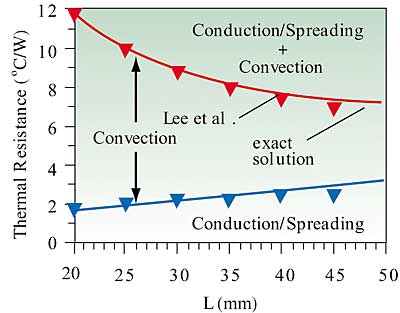Figure 6. Effect of plate length on R_tot and R_sp for a non-square thermal spreader plate.

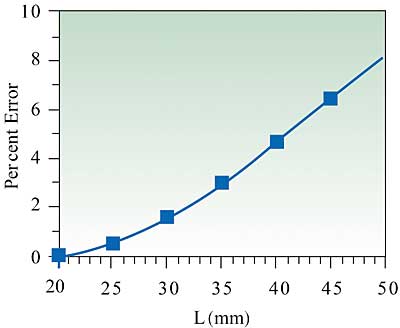Figure 7. Percent error between the exact solution and the simplified formulas vs. plate length with fixed width equal to 20.0 mm.In summary the simplified formulas developed by Lee et al. provide a very useful tool for estimating the thermal spreading resistance of a square heat source and square spreader plate geometries.

References

1. Ellison, G.N., Thermal Computations for Electronic Equipment, Van Nostrand Reinhold, New York, 1984.
2. Ellison, G.N., “Maximum Thermal Spreading Resistance for Rectangular Sources and Plates With Nonunity Aspect Ratios,” IEEE Trans. Comp., Hybrids, Manufac. Technol., Vol. 26, No. 2, pp. 439 -454, 2003.
3. Lee, S., Song, S., Au, V., and Moran, K.P., “Constriction/Spreading Resistance Model for Electronic Packaging,” Proceedings of ASME/JSME Engineering Conference, Vol. 4, 1995.