In this issue, we address the Seebeck coefficient, a property that determines the performance of thermocouples and Peltier elements. Basically, the Seebeck coefficient is related to the fact that electrons are both carriers of electricity and heat. If a temperature gradient exists over a piece of electrically conductive wire, there is a net diffusion of electrons from the hot end toward the cold end, thereby creating an opposing electric field. In (quasi) equilibrium this field causes a voltage over the wire, the so-called Seebeck voltage.
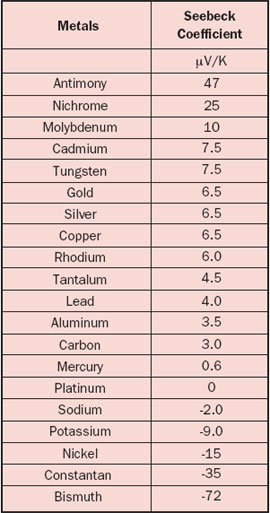
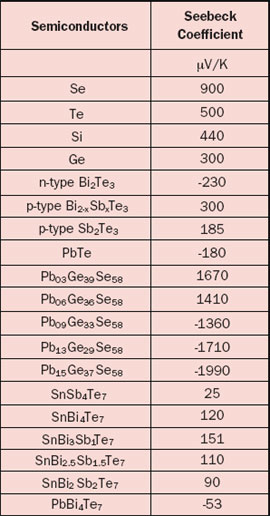
The Seebeck coefficient is defined as the Seebeck voltage per unit temperature and is a material property. However, this is not the whole story because it cannot explain the fact that the Seebeck coefficient may have different signs for different metals. The underlying solid-state physics is rather complicated but the phenomenon is well understood. The magnitude and sign of the Seebeck coefficient are related to an asymmetry of the electron distribution around the Fermi level. For example, the theory explains not only the different signs for metals but also why the Seebeck coefficient is much larger in semiconductors than in metals, as is obvious from Tables 1 and 2.
|
One should realize that the data for the materials (especially semiconductors) are prone to variation because of their sensitivity to the exact material composition. Also be aware of the fact that temperature dependency can be significant, for example a 5-10% increase for metals over a temperature rise of 30°C. It is pretty confusing that the Seebeck coefficient may be defined as an absolute value or relative to a reference material, as is the case for Table 1 where the reference material is platinum. The reason is that it is much easier to measure the relative Seebeck coefficient. To find the ‘real’ absolute values, the absolute value for Pt (i.e., 5 µV/K) should be subtracted from each value listed in Table 1.
The best choice for a thermocouple would be a combination of the highest plus and minus Seebeck coefficients. Unfortunately, many metals and semiconductors cannot be fabricated in the form of thin and robust wires. This is the main reason why commercial thermocouples are always metallic. For Peltier elements, we don’t need wires, hence semiconductor materials are the preferred choice.
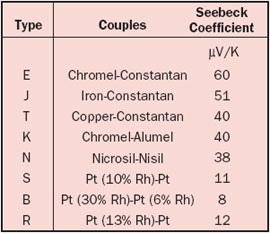
From the definition it is clear that only temperature gradients can create a voltage. If we join two wires, the total Seebeck voltage is the sum of the voltages created in the two wires. Because in an ideal thermocouple the junction is always in an isothermal region, the contribution to the thermocouple voltage is zero. In other words, the junction does not play a role other than joining the wires! More about basic thermocouple theory can be found in an article by Moffat in an earlier issue of this magazine [1]. Table 3 shows the combined Seebeck coefficient for the most popular wire pairings.
Table 3. Seebeck Coefficients for Standard Thermocouples
 |
Reference
- Moffat, R., “Notes on Using Thermocouples”, ElectronicsCooling, Vol. 3, No. 1, 1997