The analysis of convective heat transfer problems pivots on the accurate knowledge of the heat transfer coefficient, h. The heat transfer coefficient is affected by many parameters which have been defined differently by various investigators. for natural convection cases, the temperature distribution is the governing parameter, while for forced convection problems, the fluid velocity is the dominant one. For both of these conditions, the geometry of theproblem plays a significant role in determining the value of h.
Classical situations, such as flow over a flat plate or through a duct, havebeen exhaustively examined. The parameters that impact h are well known,categorized and qualified. When there is a departure from the classicalproblems in terms of the geometry and flow [1 and 2], however, predicting hbecomes a challenging endeavor. This is especially true in electronics coolingsituations, where diverse geometry and highly non-uniform wall temperatures arethe rule, not the exception.
Prediction of h is affected by its definition, the reference temperatureused to calculate it and conduction coupling through the board. Hence, threedefinitions of h are experimentally compared for their accuracy and utilityunder different conditions of non-uniform power distribution on the board [3].
Heat Transfer Coefficient Models
Convection heat transfer is described by Newton’s cooling law:
Q = hA (Ts– Tf)
(1)
where h is defined by
h = q”/(Ts– Tf)
(2)
Here q” refers to the heat flux. Ts is the surfacetemperature and Tf is some measure of the fluid temperature (in moregeneral terms, the reference temperature):
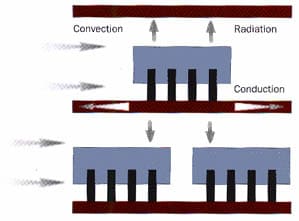
To calculate h from equation (2), the convective heat flux and theT = (Ts-Tf)must be known. The convective heat flux can be easily determined if all heelectrical input of the component goes off as convective heat transfer. Thegenerated heat is then convected away by the cooling fluid from the componentsurfaces. For a typical component, however, much of the generated heat istransferred by conduction to the board, Figure (1). To accurately calculate h,the convective portion of the heat transfer must first be determined, and thatis not a simple issue.
Figure 1: Heat transfer paths in electronicenclosures
The temperature difference in equation (2) must be carefully defined. Thesurface temperature Ts can be chosen at the hottest location, or theaverage between the hottest (centre) and the coolest (corner) temperatures, orsome other defined average over the surface. The reference temperature, Tf,is more difficult to determine, since the choice appears to be arbitrary. Inthis work, we distinguish between three different temperatures which might bemeasured.
These are:
Tin =channel inlet air temperature;
Tm = meanair temperature based on upstream power dissipation;
Tad = theadiabatic component temperature.
Tm isgiven by the following equation:
Tm = Tin+ (
/mCp)
(3)
The adiabatic temperature, Tad, is the temperature the componentwould achieve if there were no heat transfer to or from it by radiation orconduction. The adiabatic condition is theoretically important but difficult toattain in a practical situation.
Consider a component some distance inside an air-cooled channel. At thechannel entrance, the air temperature is Tin; at the considered component themixed mean fluid temperature is Tm; near the surface of thecomponent the effective average gas temperature is Tad, theadiabatic surface temperature.
The heat flux from that component can be written in the following ways:
hin = q”conv /(Ts – Tin),
(4a)
hm = q”comp /(Tcomp – Tm)
(4b)
and
had = q”comp /(Tcomp – Tad)
(4c)
Each choice of reference temperature defines a different h, and introducesdifferent problems and advantages. Tm and Tin areeither known or calculable from a energy balance, but Tad is not so easilyfound. On the other hand, hm and hin are stronglyaffected by the wall temperature distribution while had is not.
Experimental Procedure
A series of experiments were conducted to compare the effects of powerdistribution on h. The experimental setup consisted of a realistic circuit packin which the components were stimulated and placed on a typical electronicPrinted Wiring Board (PWB). This circuit pack contained an array of twelvecomponents placed in four rows (stream-wise) and three columns, Figure (2). Inthis experiment, air inlet velocity was 1.5m/s and wall to wall spacing was2.54cm.
Figure 2: Experimental setup — boardlayout and side view of the channel
Table (1) shows the powering scheme for the 12 experiments conducted. Eachcolumn corresponds to the power dissipation of a row of components. Forexample, in Case 4, power dissipation of a row of components 1, 2, and 3 was 3Watts each, components 7, 8, and 9 had 1 Watt and components 10, 11, and 12dissipated 3 Watts each. Cases 7 – 10 show the passive (power off) conditionand cases 11 and 12 are baseline tests.
The result reported here focus on components 2, 5, 8, and 11; the componentsin the center of each row, to avoid edge effects. Component 8 (the middle ofRow 3) was chosen for comparing different heat transfer definitions.
| Row –> | 1 | 2 | 3 | 4 |
| Comp –> Case V |
1,2,3 | 4,5,6 | 7,8,9 | 10,11,12 |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 3 | 3 | 3 | 3 |
| 3 | 1 | 3 | 1 | 3 |
| 4 | 3 | 1 | 1 | 3 |
| 5 | 3 | 1 | 3 | 3 |
| 6 | 3 | 3 | 1 | 3 |
| 7 | 1 | 3 | 0 | 3 |
| 8 | 3 | 1 | 0 | 3 |
| 9 | 1 | 1 | 0 | 1 |
| 10 | 3 | 3 | 0 | 3 |
| 11 | 0 | 0 | 1 | 0 |
| 12 | 0 | 0 | 3 | 0 |
| Table 1: Experimentalconfiguration and power dissipation per component in each row | ||||
Results and Discussion
The behavior of hin and hm. Figures (3) and(4) show that hin, and hm vary with row number for the 6power distributions tested. Both h’s are highly variable. Instead of themonotonically decreasing, as might be so with uniform power, hin and hm increaseor decrease sharply in response to the power distribution when the power is notuniform. For the present set of six power distributions, one could define anaverage h at each row and describe its uncertainty (about ±25%), but thatmay not be accurate enough for confident design. For these test conditions, therise in mean temperature was so small that hin and hmare essentially identical. A lower flow rate would have separated the data moreclearly. One should not conclude from these results, the hin and hmare usually so close together. In general hm > hinby an amount that increases further downstream.
 |
 |
| Figure 3: Variation of hinwith row number for six power distributions | Figure 4: Variation of hm withrow number for six power distributions |
Figure 5: Variation of h in row 3 withdifferent powering schemes
The behavior of had. These test were designed toinvestigate h in row 3 (assumed to be in the fully developed region) and had.was only measured in that one location. Hence, there are no figures showing thevariation of had with row number. Four measurements of had are shown in Figure(5). The mean value is 22.5 W / m2 °K and all four data pointslie within ±5% of the mean. This shows that had is a function of the fluidmechanics alone and is independent of the temperature distribution in thesystem. There is an interesting interpretation for had: it is the largestvalue that hm or hin could have at the point in question, for pure forcedconvection with one wall heated. This can be seen by comparing the definitions:
had = q”/ (Ts – Tad)
hm = q”/ (Ts – Tm) = q” / [(Ts – Tad)+ (Tad – Tm)]
hin = q”/ (Ts – Tin) = q” / [(Ts – Tad)+ (Tad – Tin)]
It is clear that if Tad > Tm, then had> hm. This will always be the case for forced convection withone heated wall.
Conclusions
In the present experiments, had, hm and hin weremeasured on a single component in row 3 of the array for six different powerdistributions. The results are as follows:
hin varied ±24% around a mean of 15.6 W/m2 °K
had varied 5% around its mean of 22.5 W/m2 °K
hm was substantially the same as hin (the fluidtemperature rise was too low to make a significant difference)
hm and hin are easier to measure than had but changesignificantly when the surrounding power distribution changes. If ±25%variation in h and be tolerated, or if the power distribution will not change,then hm and hin are useful.
had is more difficult to measure and to use, but is independent of the powerdistribution. This makes it attractive for incorporation into computationalcodes for calculating the temperature distribution in boards with conduction.
References
Azar, K. and Russell, E.T. Effect of Component Layout and Geometry on the Flow Distribution in Electronics Circuit Packs, Journal of Electronic Packaging; March 1991, Vol. 113, pp. 50-57.
Azar, K. Enhanced Cooling of Electronic Components byflow Oscillation, Journal of Thermophysics and Heat Transfer, 1992, Vol. 6,No. 4, pp. 700-706, 1992.
Azar, K. and Moffat, R.J. Heat Transfer Coefficient andIts Estimation in Electronic Enclosures, National Electronic Packaging andProduction Conference, pp. 361-372, Boston, MA 1991.