Estimating Parallel Plate-Fin Heat Sink Thermal Resistance

As noted previously in this column, the trend of increasing electronic module power is making it more and more difficult to cool electronic packages with air. As a result there are an increasing number of applications that require the use of forced convection air-cooled heat sinks to control module temperature. An example of a widely used type of heat sink is the parallel plate configuration shown in Figure 1.

Figure 1. Parallel plate fin heat sink configuration.

In order to select the appropriate heat sink, the thermal designer must first determine the maximum allowable heat sink thermal resistance. To do this it is necessary to know the maximum allowable module case temperature, T_case, the module power dissipation, P_mod, and the thermal resistance at the module-to-heat sink interface, R_int. The maximum allowable temperature at the heat sink attachment surface, T_base, is given by

The maximum allowable heat sink resistance, R_max, is then given by

where T_air-in, is the temperature of the cooling air at the inlet to the heat sink passages. At this point many thermal engineers will start looking at heat sink vendor catalogs (or more likely today start searching vendors on the internet) to find a heat sink that will fit in the allowable space and provide a heat sink thermal resistance, R_hs, less than R_max at some specified flow rate. In some cases, it may be useful to do a sizing to estimate R_hs for various plate-fin heat sink designs to determine if a feasible design configuration is possible. The remainder of this article will provide the basic equations to do this. The thermal resistance of the heat sink is given by

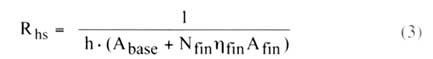where h is the convective heat transfer coefficient, A_base is the exposed base surface area between fins, N_fin is the number of fins, _fin is the fin efficiency, and A_fin is the surface area per fin taking into account both sides of the fin.

To proceed further it is necessary to establish the maximum allowable heat sink volume in terms of width, W, height, H, and length in the flow direction, L. It is also necessary to specify a fin thickness, t_fin. Using these parameters the gap, b, between the fins may be determined from

The exposed base surface area may then be determined from

and the heat transfer area per fin from

At this point it is necessary to specify the air flow rate either in terms of the average velocity, V, between the fins or a volumetric flow rate, G. If a volumetric flow rate is used, the corresponding air velocity between the fins is

To determine the heat transfer coefficient acting upon the fins, an equation developed by Teertstra et al. [1] relating Nusselt number, Nu, to Reynolds number, Re, and Pr number, Pr, may be employed. This equation is

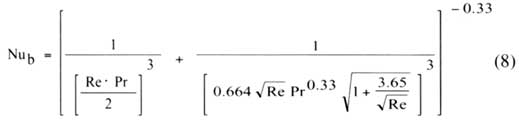The Prandtl number is

where is the dynamic viscosity of air, c_p the specific heat of air at constant pressure, and k is the thermal conductivity of air. The Reynolds number used in (8) is a modified channel Reynolds number defined as

where is the density of air. Equation (8) is based upon a composite model spanning the developing to fully developed laminar flow regimes and was validated by the authors [1] by comparing with numerical simulations over a broad range of the modified channel Reynolds number (0.26 <Re_b < 175) and with some experimental data as well. Using the Nusselt number obtained in (8) the heat transfer coefficient is given by

where k_fluid is the thermal conductivity of the cooling fluid (i.e. air). The efficiency of the fins may be calculated using

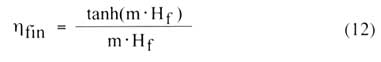where m is given by

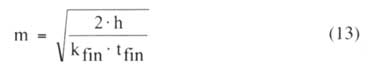and k_fin is the thermal conductivity of the fins.

Using these equations it is possible to estimate heat sink thermal performance in terms of the thermal resistance from the temperature at the base of the fins to the temperature of the air entering the fin passages. It may be noted that the relationship for Nusselt number (8) includes the effect of the temperature rise in the air as it flows through the fin passages. To obtain the total thermal resistance, R_tot, to the base of the heat sink it is necessary to add in the thermal conduction resistance across the base of the heat sink. For uniform heat flow into the base R_tot is given by

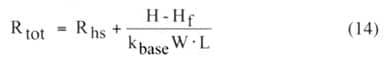and k_base is the thermal conductivity of the heat sink base.

For purposes of illustration these equations were used to estimate heat sink thermal resistance for a 50 x 50 mm aluminum heat sink. The effect of increasing the fin height and the number of fins is shown in Figure 2 for a constant air velocity and in Figure 3 for a constant volumetric flow rate. In both cases it may be seen that there are limits to how much heat sink thermal resistance may be reduced by either increasing fin length or adding more fins. Of course to determine how a heat sink will actually perform in a specific application it is necessary to determine the air velocity or volumetric flow rate that can be delivered through the heat sink. To do this it is necessary to estimate the heat sink pressure drop characteristics and match them to the fan or blower to be used. This is a topic for consideration in a future article.

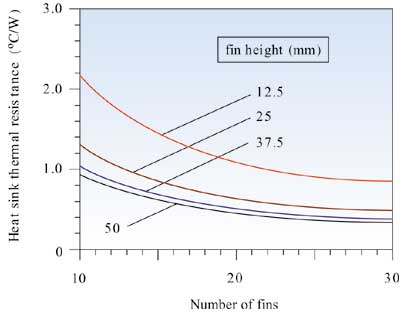Figure 2. Effect of fin height and number of fins on heat sink thermal resistance at an air velocity of 2.5 m/s (492 fpm).

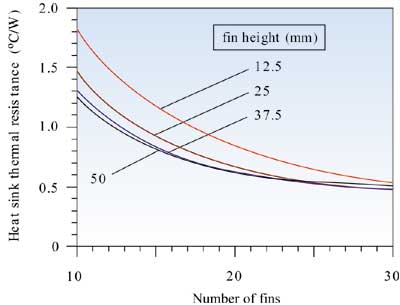Figure 3. Effect of fin height and number of fins on heat sink thermal resistance at a volumetric air flow rate of 0.0024 m³/s (5 CFM).

References

1. Teertstra, P., Yovanovich, M.M., and Culham, J.R., “Analytical Forced Convection Modeling of Plate Fin Heat Sinks,” Proceedings of 15th IEEE Semi-Therm Symposium, pp. 34-41, 1999.