The heat transfer coefficient is used to describe convective heat transfer between a solid and a fluid, as in Equation (1).
The heat transfer coefficient is a defined parameter, not a physical property like thermal conductivity, and different definitions are used for different situations. The preferred definition for use in the electronics-cooling situation is hadiabatic, in which the fluid temperature is described by Tadiabatic, the adiabatic temperature of the component.
Unfortunately, the definition most heat transfer people use for internal flow heat transfer is hmean, where the fluid temperature is described by Tmean, the mixed mean temperature of the coolant. I say “unfortunately” because most electronics cooling folks take values of h from the electronics cooling literature to be values of hmean, and use them with Tmean to predict operating temperatures. That doesn’t work because almost all reported values are for hadiabatic, not hmean. Using a value of hadiabatic with Tmean will under-predict the operating temperature.
What Is Tadiabatic and Why Is It Better Than Tmean?
The adiabatic temperature of a component is the effective temperature of the coolant as far as that component is concerned; it is the average temperature of the coolant that actually touches the component. The mean temperature has nothing to do with heat transfer to the component: the coolant touching the component is not at the mean temperature. In a research lab, or in a CFD code, the adiabatic temperature of a component can be determined by isolating the component (no net energy in or out) while holding all other components at their normal operating temperatures. The component then “floats” in the coolant stream and takes on the average temperature of the coolant that touches it. In a running system, Tadiabatic may be different for components that are side-by-side!
What Are the Operational Benefits of hadiabatic Over hmean?
There are several:
1- Thinking in terms of hadiabatic and Tadiabatic keeps expectations in line with reality.
Consider a component running at 100°C in a situation where the adiabatic temperature is 60°C and the mean coolant temperature is 30°C.
Question: If that component’s power were cut by 50%, how much would its temperature drop?
Answer: It would drop 20°C.
The value of hadiabatic is determined by the system geometry and the flow field and it will not change when the power level changes – you can count on that. Therefore, dropping the power by 50% will drop (To-Tadiabatic) by 50% – it will not drop (To-Tmean) by 50%. When the power goes down, hmean goes down.
2- Thinking in terms of had displays a new tool for solving cooling problems.
Let us expand Equation (1) into a more useful form – one that can only be used when using hadiabatic (because only hadiabatic stays constant when the heat release changes.):
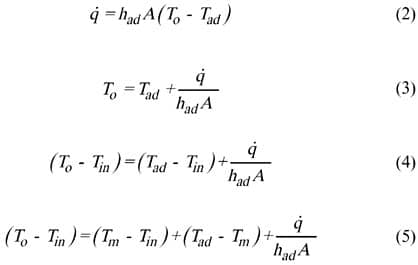 |
Equation (4) expresses the temperature rise of the component above the inlet temperature of the coolant as the sum of three terms that can be independently measured or calculated:
- The mean fluid temperature rise, (Tm-Tin)
- The elevation of the adiabatic temperature above the mean temperature, (Tad -Tm)
- The self-heating temperature rise of the component,
/ hadA
Thus, thinking with hadiabatic reveals that there are three ways to approach an overheating problem, not just one:
- Reduce the mean temperature rise (increase the flow)
- Reduce the elevation of Tadiabatic (improve the cross-stream mixing)
- Reduce the self-heating temperature rise (increase had by increasing the turbulence intensity or the flow)
Surprisingly often, the biggest contributor to over-temperature is not the self-heating term, which is the only one involving h, but the elevation of Tadiabatic over Tmean caused by stratification in the coolant. In those cases, the system benefits more from improving the mixing than it would have from increasing the flow.
Note that if you consider this same situation using hmean with Equation (1), the only way to reduce the operating temperature appears to be to increase h. There is no hint of the benefit that might come from improving the mixing.
3- One final reason to think in terms of hadiabatic, quite compelling in its own right, is that all of the experimental h-data in the electronics cooling literature is had.
Almost all of the experimental data in the literature come from “single active element” tests: one active element in an otherwise passive array. Such tests implicitly define h as hadiabatic, whether that is mentioned in the paper or not. If you use those values with Tmean, you will under-predict the operating temperature.
Some Closing Notes
The benefits of describing heat transfer in terms of hadiabatic and Tadiabatic are not limited to electronics cooling situations. These ideas can be profitably applied to any convective heat transfer situation – free, forced, or mixed. For example, a boundary layer code that calculates heat transfer can be adapted to evaluate hadiabatic. The code needs to learn only one new trick: after each stream-wise step, it must first set = zero on the next x-interval and calculate the adiabatic surface temperature for that interval. Then it must set the surface temperature to its specified temperature and calculate the heat transfer in a normal manner. The value of hadiabatic can then be found, step by step, along the surface since
and Tadiabatic are both known.In many situations involving steps or rapid stream-wise changes in wall temperature, we would like to know how the heat transfer rate changes with position along the surface. In classical heat transfer, that is a difficult problem. Thinking in terms of hadiabatic, the shape of the solution can often be estimated quite accurately (and sometimes the values). Whether its value is known or not, one thing you can trust is that a value of hadiabatic exists at every point and it does not change when the surface temperature changes.
For example: Why is the heat transfer rate higher, point for point, if the wall temperature is increasing in the flow direction than it would have been, at the same point, if the wall temperature had been uniform? It is higher because at each step in the x-direction, the adiabatic temperature is lower than it would have been with a uniform wall temperature (at the local value). The local adiabatic wall temperature is always set by the upstream conditions. The value of hadiabatic is fixed and since the difference (To-Tad) is larger, the heat transfer rate is larger.
There are many more examples that could be discussed in gas turbine blade and vane heat transfer, and in predicting the altitude performance of electronics cooling systems. In June 1995, Kaveh Azar and I illustrated the advantages of hadiabatic in an article published in ECM, available online in the resources section of www.electronics-cooling.com.






