Introduction
In the past 15 years, we have observed a significant increase in the use of Computational Fluid Dynamics (CFD) codes to calculate the thermal behavior of electronic systems. The benefits are undisputed when it comes to performing parametric studies in early design phases. However, when the objective is accuracy, the discussion about what we can expect in practice becomes far from trivial. The heat transfer behavior of electronic systems is very complex when compared to the standard canonical cases usually treated in fluid dynamics classes. A natural question is how accurate numerical simulations are when compared to well-designed experiments. Many studies demonstrate amazing agreement, the conclusion often being that ‘validation of the numerical model’ has been proven. It will be demonstrated that these conclusions are subject to serious doubts. The major reason is the lack of sufficiently accurate input parameters and boundary conditions combined with complex geometries.
This article – which is a compilation/extension of a 17-page paper by the same author [1] – focuses on the following question: Can we really predict the junction temperature of critical components in a complex system with sufficient accuracy? The conclusion is: not without fitting!
The Difference between ‘Validation’ and ‘Calibration’
Regarding numerical analysis, the word ‘validation’ is frequently used in different contexts. We should distinguish between verification, validation and calibration.
- Verification relates to solving the equations correctly.
- Validation relates to testing of predictive capabilities of physical models against detailed test data, including convergence.
- Calibration relates to fitting a model in such a way that e.g. temperatures are predicted to a sufficient degree of accuracy.
In this context, most authors mean ‘calibration’, not ‘validation’.
Uncertainties
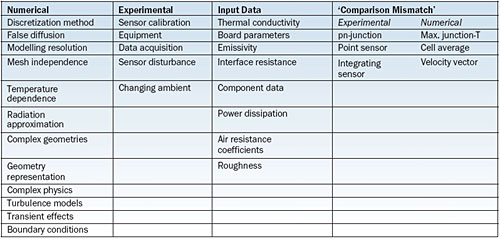
Table 1 summarizes the various types of uncertainties that influence a comparison between numerical and experimental results.
Table 1. Types of Uncertainties
Numerical Uncertainties
Accuracy (defined as predicted over true temperature rise) is influenced by the chosen discretization method, false diffusion, temperature-dependent physical properties, the Boussinesq approximation, the convergence criteria, and the geometric representation of a real object in a database. These uncertainties will decrease in the future because almost all approximations can be relaxed by using a more powerful computer. However, the discretization error will stay for some time because it is still impossible in practice to model every boundary layer in order to capture the local heat transfer correctly. The radiation error suffers from another problem. All engineering calculations are based on the following assumptions:
- All surfaces are diffuse (or, sometimes, specular), grey, opaque and uniformly irradiated.
- The medium between surfaces is transparent for the wavelength ranges of interest.
Especially the first generalization may cause unrealistic over-simplifications in applications dominated by natural convection (or vacuum). The ultimate challenge for an accurate numerical analysis, however, is posed by the modelling of a few complex physical phenomena that are inherently present in a real system. It is in this area that the largest errors are often made, caused partly by the discrepancy between reality and the modelling assumptions, and partly by the user’s lack of awareness. Maybe the most challenging task is to model the very complex boards with their multiple planes, vias, tracks and solder bumps. Not covering all details may result in significant errors [2]. The global Printed Circuit Board (PCB) effective thermal conductivity is often used to fit the model, unfortunately, authors rarely mention this.
Instabilities and ‘mini-jets’ generated by a grille are never modelled but these effects persist long enough to cause a measurable influence on downstream local heat transfer. Other largely unknown parameters are the local heat transfer coefficients at the outside envelope of the system. Values taken from any textbook would usually serve our goals. There are exceptions, however. Systems with a large bottom surface area may transfer a significant amount of heat to the support. The presence of heated horizontal plates induces another source of error that is difficult to address because of potential instabilities. Two examples are given, more in [1].
- A minor disturbance in an otherwise steady state operating system could cause a transition to a completely different flow field in an unpredictable way.
- If more than one power source contributes to the heat transfer, the resulting flow field could depend on the sequence of powering up.
Transitional and turbulent convection pose another problem. Sophisticated turbulence models are not expected to be implemented in system-level analysis design tools for quite some time. To capture low-Re transitional flow requires a very fine grid and time-dependent analysis. A recent article [2] discusses this topic in more detail and concludes that significant errors are unavoidable. A last complex issue that deserves attention is the modeling of fans. Certainly not every detail of a fan, both dimensionally and a velocity-wise, can be taken into account in a system level analysis in the foreseeable future. Hence, accurate prediction of the local heat transfer coefficients is out of the question.
Experimental Uncertainties
In general, most of the experimental errors can be reduced to a level that is adequate given the objective of the analysis. It is instructive to distinguish between ‘what is measuring’, ‘what is being measured’ and ‘what is desired’. The first point refers to the chain sensor → measuring equipment → data acquisition. The errors associated with temperature measurement can be limited to 0.1°C or less, if some precautions are taken. However, even if this type of error is zero, the other parts usually cause many more problems, as the effects are often not recognized. In [1] a long list of what may go wrong is presented. For example, a thermocouple may act as a cooling fin. With ongoing miniaturization, this becomes an increasing problem.
Input Parameter Uncertainties
For a fair comparison between experimental and CFD results all input parameters should ideally be known to within a few percent of the final uncertainty. In general, the uncertainty caused by variations in material properties is much easier to assess than the errors caused by the modelling of complex fluid flow phenomena. As a rule of thumb, the material properties of the electronic parts that are closest to the component whose temperature is to be studied have the strongest impact. Hence, by far the greatest problems are caused by the uncertainty of the package and board properties. While in theory the designer can control all parameters, the exception is the thermal data acquired from the component manufacturer.
Thermal Conductivity
Unfortunately, no accurate data is available for many engineering materials, let alone as a function of temperature. Many engineering materials also exhibit anisotropy, and most standard tests only measure in one direction. In other words, because 3D conduction heat transfer dominates in practice, even a very accurate value obtained from a standard lab does not guarantee accuracy in a practical application.
A related fact is that the wrong values are often used, especially for materials with large temperature dependence such as silicon. Using the value for Si at room temperature while calculating the thermal behaviour of a package at operational temperature can easily result in an error of 20%.
An especially intriguing problem shows up when printed circuit boards are part of the analysis. Unfortunately, many commercially available thermal software packages calculate an average conductivity using a series and parallel thermal resistance approach, not taking into account the order of the layers.
Let us assume that 50% of the heat transfer of the metal block is by conduction via the board (for surface mounted components without a heat sink, this value can easily be 80%). A 20% error in the thermal conductivity results in a 10% error in prediction of the package-board assembly temperature rise.
Emissivity
Apart from the difficulties as discussed earlier, there is another problem that impedes an accurate radiation analysis: oxide layers, roughness, surface treatment, scratches, and dust, all significantly influence the surface emissivity. This is precisely why it is often useless to look up the values in textbook tables unless rough estimates are the objective of the calculation. A final point is that practical surfaces tend to deteriorate with time, due to oxidation and settling of dust.
When radiation heat transfer accounts for 20% of the total heat transfer, which is a commonly encountered situation in natural convection cooling, and when the emission coefficient has an error of 25%, a 5% error in the calculated temperature results (provided the radiation model is correct!).
Interface and Contact Resistances
Component manufacturers have succeeded in achieving a continuous decrease in the package’s overall thermal resistance. Indeed, the influence of the interface resistance starts to dominate. Unfortunately, vendor data is not reliable [3]. As the theoretical treatment of contact heat transfer is still very difficult, we have to rely on experiments. With the right equipment, it is possible to keep the errors well under 5%. The problem is that few labs have the right equipment.
If the interface accounts for 50% of the total resistance and the error in the resistance is 20%, the resulting contribution to the inaccuracy of the junction temperature is 10%.
Thermal Data Provided by Component Manufacturers
Many papers have recently been published dealing with so-called boundary-condition-independent compact models [4,5], aimed to replace the existing thermal data sheets. These models, usually in the form of a simple resistance network, can be embedded in board and system level analysis software. It has been demonstrated for many package families that their inaccuracy is less than 5% compared to the detailed models. As long as these models are not available, the use of ‘standard’ thermal data provided by the component manufacturers can easily result in errors of 30% or more.
Power Dissipation
An important parameter (often misused to match experimental and numerical results) is the power dissipation of active devices. In some cases it is relatively easy to know the dissipation by measuring currents and voltages. In other cases it is virtually impossible. Errors in the estimated dissipation have a one-to-one correspondence with junction temperature errors. Another important factor is the assumption about the power distribution over the active surface of the die. Standard practice is ‘uniform’, however, this is a pretty conservative assumption.
Roughness
Surfaces are often treated as smooth, but are in fact hydrodynamically rough, especially at the leading edge of components where the boundary layer is very thin. For example, traces on circuit boards are raised as the copper is deposited onto the FR4 (e.g., the roughness height is 35�m.)
Mismatch Uncertainties
A special class of uncertainties concerns those that are related to a mismatch between what is measured and what is calculated. The temperature of silicon is often measured using the voltage-temperature dependence of suitable p-n junctions. However, these junctions are not usually located at the spot where the maximum temperature occurs. A significant temperature difference may result, particularly for power devices. Adequate comparison between numerical simulation and the experiment can only be realised when the location of the pn-junction is also modelled, which requires an unrealistic mesh.
Another example: usually a thermocouple reading is compared with some average grid cell temperature. If the sizes don’t match, there is a clear discrepancy if large temperature gradients are present.
Errors When Comparing Numerical and Experimental Results
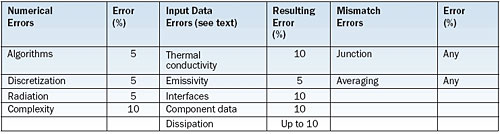
Let us consider the situation that substantial differences are found between the results of CFD analysis and experiments. Let us further assume that the experiment is well designed, so that the results are correct to within 5%, based on 20:1 odds. The question arises: How accurately are the real physics simulated by the numerical analysis and how accurately are the physical properties and input parameters known? Table 2 provides plausible uncertainty contributions to the calculation of junction temperatures.
Table 2. Estimated State-of-the-Art Contributions to Uncertainty in Junction Temperature
How to Improve?
We may expect that on the numerical side some errors will decrease to more acceptable levels. The errors related to the treatment of complex fluid phenomena will not be reduced to the same extent unless Direct Numerical Simulation (DNS) or Large Eddy Simulation (LES) techniques become feasible for 3D complex systems. While it is true that some improvement could be gained by implementing more sophisticated turbulence models [2] it is by no means a panacea for the problems mentioned. Suppose we want to model spray cooling. It makes a lot more sense to design appropriate experiments to estimate the local heat transfer instead of relying on very complex 3D highly turbulent two-phase CFD simulations. One way to enhance the predictability of CFD analyses is to use a pragmatic approach by employing correction factors. A recommended way to measure correction factors is by developing ‘ideal’ experimental benchmarks for complex geometries where all boundary conditions and material properties are under control and are well known to within a few percent [1].
Conclusions
The continually shrinking time-to-market for electronic products will require an ever-increasing reliance on computational simulations. However, a number of issues still impede a greater reliance on predictive modelling capabilities. In particular:
- Computational resources for handling large, realistic problems
- Databases on thermophysical properties of electronic packaging materials
- Accurate in-situ determination of physical properties
- Assessment of interface thermal resistances
- Wide availability of compact models supplied by vendors
- Accurate benchmarks to assess and correct the influence of complex geometries
The most important conclusion emerging from this article is: A numerical analysis of an electronic system may or may not be correct, and no one can tell. Suppose the calculated and measured junction temperatures differ by 20%, then it is still possible that both analyses are correct to within 5% or better, simply because sufficiently known input data are lacking. Another way to put it: An accurate match (� 10%) is not possible without some kind of fitting. Despite the conclusions, CFD tools are vital in design environments! However, do not expect or claim high accuracy in a direct comparison with experiments.
References
- Lasance, C., “The Conceivable Accuracy of Experimental and Numerical Thermal Analyses of Electronic Systems”, IEEE CPT 25, 2002, pp. 366-382.
- Rodgers, P., Eveloy, V., “CFD Prediction of Electronic Component Operational Temperature on PCBs”, ElectronicsCooling, Vol. 10, No. 2, 2004, pp 22-28.
- Lasance, C., “Problems with Thermal Interface Material Measurements: Suggestions for Improvement”, ElectronicsCooling, Vol. 9, No. 4, 2003, 22-29.
- Lasance, C., “Recent Progress in Compact Thermal Models”, Proceedings SEMITHERM XIX, San Jose, CA, 2003, pp. 290-299.
- Sabry, N., “Higher-Order Compact Thermal Models”, Proceedings THERMINIC X, Sophia Antipolis, 2004, pp. 273-280.