Heat Spreading: Not a Trivial Problem

 Introduction

Heat spreading is essentially area enlarging: the larger the area, the more heat can be removed at the same temperature difference (subject to certain limits). Unfortunately, except for the simplest of cases, the equations describing heat spreading physics do not have an explicit mathematical solution. Hence, we have to rely on clever approximations or suitable computer codes. This article discusses the basics of heat spreading starting with the problematic definitions of thermal resistance and maximum allowable flux.

The Thermal Resistance Conundrum

Thermal resistance data published by vendors are widely used to compare the performance of various products, be it semiconductor packages, LEDs or heat sinks. The common notation is:

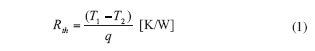However, we rarely have constant temperatures at the two faces where the heat flux originates and where the same flux leaves. Here is a formal definition of thermal resistance:

The temperature difference between two isothermal surfaces divided by the heat that flows between them is the thermal resistance of a) the materials enclosed between the two isothermal surfaces and b) the heat flux tube originating and ending on the boundaries of the two isothermal surfaces [1].

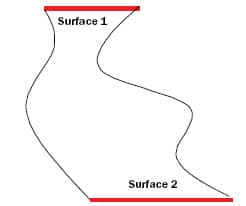Figure 1. Two isothermal surfaces connected by a heat flux tube.

The emphasis is on ‘isothermal surfaces 1 and 2’ and ‘flux leaving 1 equals flux entering 2’, see Figure 1. Now consider Figure 2 showing two simple cases of heat spreading where all surfaces are adiabatic except the bottom surface.

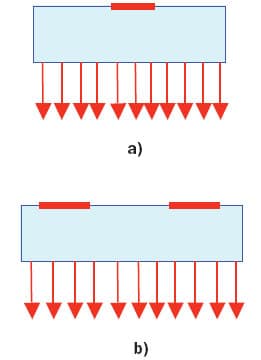Figure 2. Heat spreading from single source (left) and two sources (right).

For the single source case a constant heat transfer coefficient h at the bottom causes a non-uniform temperature profile on this face, except in the case of h or the thermal conductivity k being infinite or the trivial case of the source area equalling the substrate area. The average temperature could be used but the question in practice is: how do we get this value? Usually one thermocouple is used at the center, but one should realize that the thermal resistance from source to thermocouple defined in this way is by definition dependent on the boundary conditions because these determine the temperature profile and hence the temperature at the location of the thermocouple.

The only definition that is in accordance with the definition is the thermal resistance from source to ambient: R_thj-a, but this value is often useless because the boundary conditions are rarely the same. However, even this definition is lost when more than one source is present, such as in Figure 2b, because the main condition for a correct definition, the fact that the same flux has to enter and leave the resistance, cannot be fulfilled. The essential point to understand is that the concept of thermal resistance becomes meaningless when dealing with multiple sources. It is theoretically possible to solve this problem because the substrate can be split in such a way that every source has its own volume allocated to it (based on the minima of the isotherms) but then the simplicity of the concept is lost.

A possible way out is to make use of the principle of superposition. By switching off all sources except one we are able to find again the thermal resistance from that source to ambient. However, its use for design purposes is limited because the problem cannot be reduced to a parallel combination of all individual source-ambient resistances found in this way, put otherwise: no network can be constructed using these resistors. It might serve however as a way to thermally characterize multisource applications by providing a test protocol.

The Flux Conundrum

Let’s calculate how much heat we may dissipate by natural convection at a Δ T of 50�C. We may write for the flux =hΔT, and with h=12 W/m²K (including radiation) we get =600 W/m². The conclusion is then: natural convection can handle 600W/m². Is this correct? Yes and no. Can we put 60 mW in one square centimeter? Yes, no problem. Can we put 600 W in one square meter with a source of a few cm² and stay within the quoted temperature limit? No, we can’t, because the simple equation assumes not only a uniform h but also a uniform surface temperature. The problem is caused by the fact that we are dealing with increasing temperature gradients over the surface when the area increases.

Why do we always talk W/cm²? Because the thermal management field is dominated by the cooling of processors that have dissipating areas of O(cm²). Now take a junction of such a processor. The area is about 0.1*0.1�m and with 1 �W dissipation this comes down to an amazing 10kW/cm². Nobody has a problem with this. Apparently it is the dissipating area that sets the limit to the maximum allowable flux. A useful rule of thumb has been formulated by Willcoxon and Cornelius [2], using the following equation:

However, its use is limited to areas larger than about 0.1*0.1 mm². It should also be realized that this limit depends not only on the source size but also on the spreader thickness, area, thermal conductivity and boundary conditions. In summary, what is important to realize is that it does not make sense to use the same heat flux limits for both processors and LEDs alike. The author suggests to quote the “raw” data related to the size of the source: e.g.; for a junction, W/�m²; for a die, W/cm²; for a TV backplane, W/m².

Basic Principles of Heat Spreading

Single Source, Single Layer

Contrary to what is believed by many designers: heat spreading is not a trivial issue. Consider the simple configuration shown in Figure 2. A square source with zero thickness of size A_s centrally located on a square plate of size A, thickness d and thermal conductivity k dissipates q W. The top and sides of the plate are adiabatic (insulated), the bottom ‘sees’ a uniform heat transfer coefficient h (W/m²K). The remarkable thing is that even for this simple configuration no explicit solution is known for the description of heat spreading.

Observing the exact implicit solution of the governing differential equations reveals the source of the complexity of heat spreading: it is not possible to separate the convection and conduction parts. In other words, changing the heat transfer coefficient changes also the value of the spreading resistance. Consequently, it is not possible to write the problem in terms of one conduction resistance describing the heat spreading inside the solid and one convection resistance describing the boundary condition because the two are dependent.

There is one exception: the analysis becomes much more straightforward when the temperature gradients over the area that is in contact with the environment can be neglected. In other words, a uniform temperature may be assumed. Such is often the case with relatively small heat sinks and spreaders.

A final complexity stems from the fact that decreasing the thickness of the plate does not automatically result in a decrease in temperature, caused by the fact that a smaller thickness also implies a decrease in spreading capability. Hence, for a certain combination of thickness and thermal conductivity, given the boundary conditions and the dimensions, a minimum in the total thermal resistance may be found.

Single Source, Multiple Layers

In practice we often have to deal with multiple layers.

Figure 3. Cross section through one planar source on a submount and a heat spreader.

Figure 3 shows a cross section of a single source on a submount, which is itself connected to a second spreader. Closer observation reveals two heat spreading effects: one from submount to spreader, and one from the source to the submount. To first order, this problem can be handled as a single layer problem, provided the boundary condition of the first layer is replaced by the spreading plus the boundary condition of the second layer.

Multiple Sources

Multiple sources add another layer of complexity because the coupling between the sources is not only dependent on the dimensions and physical properties but also on the boundary conditions and, worst of all, on the dissipation of the sources themselves. Using superposition techniques is the recommended approach.

Approximate Heat Spreading Solutions for the Single Source-Single Layer Problem

In the following, three approximate solutions will be discussed.

The 1D-Series-Resistance Approach

Equation 3 describes the temperature rise of the source due to dissipation q via a total thermal resistance R_total from junction to ambient. While it is physically correct, splitting up this resistance according to equations 4 and 5 is not.

with g=f (A_s, A) some geometrical factor representing the spreading, e.g., the 45� rule.

The L-Equation

A long time ago, the author derived a simple rule-of-thumb for the case of a single source on a plate with uniform heat transfer coefficients at both sides, mainly for flat heat sinks [3]. The assumptions are that a surface source can be replaced by a volume source extending over the thickness and that a square plate can be replaced by a flat cylinder. Surprisingly, it turned out that the equation is valid over quite a large range of parameters, including low-conductivity substrates and even non-square areas up to a length/width ratio of 4. By approximating the Bessel-function solution for the cylinder by algebraic equations, the following equation results for one-sided heat transfer:

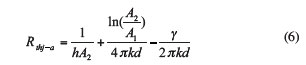where γ is Euler’s constant, 0.577. With some care, the first term of the right-hand side could be interpreted as a convective term, the second as a conductive term, and the third as a correction term. Note: due to the negative sign this equation does not represent a simple series resistance network.

To guarantee an accuracy of better than 90% the following inequalities should be obeyed:

m is the so-called fin factor, and a and b equivalent radii for respectively source and base area, defined as:

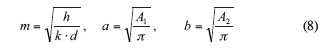For non-centrally placed sources it can easily be shown [4] that simple correction factors can be applied. Calling the first term in Eq. (6) C₁ and the second plus third C₂, it follows:

For a source in the corner, the extra Δ T is given by 3�C₂�q (exact). For a source at the center of a side, the extra Δ T is C2�q (approximation). More sophisticated correction factors can be found in an article by Lee [5].

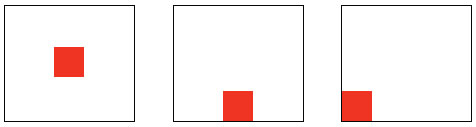Figure 4. Position of source: center, side, corner.

The SLA-Equations

Song et al. [6] and Lee et al. [7] found a set of approximate explicit formulae that are easy to implement in a spreadsheet. They showed that the errors stay within 5% or less for the majority of cases of practical interest. The maximum spreading resistances is defined as:

where is the average temperature of the base area. Approximate equations are presented to calculate not only R_max but also R_avg, based on the average temperature of the source. The interested reader may consult the references cited. Finally, the temperature rise from junction to ambient is calculated using:

At first sight this expression looks like an ordinary series resistance network. However, it should be understood that R_max is a function of the boundary conditions, contrary to the networks discussed previously.

(Author’s Note: For the reader who wants to consult the original papers a word of caution should be issued because the three relevant papers differ in the definition of the parameters. In [6], the 1D conduction resistance and the spreading resistance are separate entities and R_max is only associated with the spreading resistance. In [7], R_max is defined as the sum of the two. The result is different graphs. In [5], equation (1) is only correct if R₀ equals R_conv. However, formally R₀ represents the sum of R_conv and R_1D (R0 =1/hA+t/kA). Fortunately, in most cases the errors are negligible, but for those cases with h/k > 100 and d > 10 mm the errors are of the order of 10% and beyond. However, especially the condition d > 10 mm is not likely to occur in practice.)

In summary, heat spreading is a complex phenomenon that can be addressed by analytical formulae only for geometrically simple cases for which no explicit solution exists. For situations where double -sided heat transfer plays a role, or multiple sources, or multiple layers, the problem becomes intractable from an approximate analytical point of view and we have to rely on computer codes. Implicit solutions are known for multi-layer cases with multiple sources and uniform boundary conditions, even when time is a parameter.

User friendly software exists that is based on these solutions, with the additional advantage that no mesh generation is required [8]. The big advantage of such software is that even people with little background in heat transfer can get insight in the physics underlying heat spreading by simply changing a few parameters. For the more practical cases for which layers consist of more than one material or for which the boundary conditions cannot be considered uniform, more advanced conduction-only codes should be used. Another recommended source of information can be found on the website of the University of Waterloo [9]. One of their papers [10] shows a couple of graphics showing clearly the errors a designer may encounter by using equations such as Eq. (5).

What Errors Can Be Expected?

An important question is: what are the errors if we use the approximate formulae? A detailed analysis will be presented in the future, here are the most important conclusions.

Conclusions for Single layers

• The 1D approximations should not be used at all.
• The L-equation can be used, provided h/k�d < 0.025; e.g., h = 2500 W/m²K, k = 100 W/mK, d = 1 mm: h/k�d = 0.025.
• The SLA equation can be used over a very large range.
• It is strongly recommended to use a user-friendly code.

 

Conclusions for Two Layers

• The 1D approximations should not be used at all.
• While the L-equation is accdeptable for a certain range, its use is not recommended because too many conditions have to be met to guarantee accurate values.
• The SLA-equations can still be used over a very large range but errors increase when h/k > 10, k_subm > 100 W/mK and d < 1mm
• It is strongly recommended to use a user-friendly code.

 

Conclusions for More Than One Source

• Be careful using simple resistance networks.
• Use superposition.
• Use a matrix-approach for thermal characterization.

 

Conclusions for All Other Cases

• Use a conduction-only code.

 

Conclusions

The author hopes he succeeded in conveying the message that heat spreading is not a trivial problem that can be solved by simply adding convective and conductive thermal resistances. A physically correct spreading resistance may be formulated, but it always contains the convective boundary condition. Unfortunately, the notion of a thermal spreading resistance fails when we are dealing with multiple sources and we have to rely on more sophisticated matrix methods.

References

1. Rosten, H. and Lasance, C., “DELPHI: the Development of Libraries of Physical Models of Electronic Components for an Integrated Design Environment,” in Model Generation in Electronic Design, Eds.: Berge, J-M., Levia, O. and Rouillard, J., Kluwer Academic Press, 1995, pp. 63-90.
2. Wilcoxon, R. and Cornelius, D., “Thermal Management of an LED Light Engine for Airborne Applications,” Proc. SemiTherm 22, Dallas, 2006, pp.178-185.
3. Lasance, C., “Computer Analysis of Heat Transfer Problems to Check the Validity of Engineering Formulae,” Proc. 8th IHTC, San Francisco, 1986, pp. 325-330.
4. Lasance, C., “Pragmatic Methods to Determine the Parameters Required for the Thermal Analysis of Electronic Systems,” in ‘Cooling of Electronics’, Eds.: Kakac, S., et al., Kluwer Academic Publishers, 1994, pp. 859-898.
5. Lee, S., “Calculating Spreading Resistance in Heat Sinks,” ElectronicsCooling, Vol. 4, No. 1, January, 1998.
6. Song, S., Lee, S. and Au, V., “Closed-Form Equations for Thermal Constriction/Spreading Resistances with Variable Resistance Boundary Condition,” IEPS Conference, 1994, pp. 111-121.
7. Lee, S., Song, S., Au, V., Moran, K., “Constriction/Spreading Resistance Model for Electronics Packaging,” ASME/JSME Thermal Engineering Conf., Vol.4, 1995, pp.199-206.
8. http://www.micred.com/therman/
9. http://mhtlab.uwaterloo.ca/RScalculators.html
10. Culham, J. and Yovanovich, M., “Factors Affecting the Calculation of Effective Conductivity in Printed Circuit Boards, Proc. ITHERM ’98, Seattle, 1998, pp.46-467.