Radiation heat transfer can be a significant portion of total heat transfer from a heat sink, particularly in natural convection flows. The enclosures for most natural-convection-cooled indoor and outdoor electronic equipments, such as pole or wall-mount base stations and radio units, include external fins to improve natural convection and radiation heat transfer rates. Early design of these types of equipment usually involves extensive iterations to come up with an optimum fin arrangement that provides the required heat dissipation capability with minimum dimensions and weight. Simple analytical correlations can be very useful for this purpose.
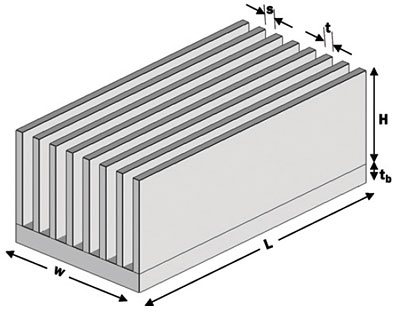 |
Figure 1. A typical plate-fin heat sink.
Consider the plate-fin heat sink shown in Figure 1. The total radiation heat transfer rate from this heat sink is equal to the sum of the radiation heat transfer rates from the U-shaped channels between pairs of neighboring fins, the fin tips, the fin front and rear sections, the outside surfaces of the outer fins, and the peripheral surface of the heat sink base. If we assume that the heat sink surface is diffuse and gray, the surrounding medium is very large and/or a black body at temperature Tsurr, and the heat sink is at uniform temperature Ts, the total radiation heat transfer rate from this heat sink is
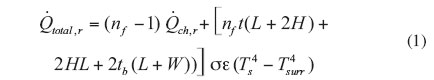 |
where ch,r is the radiation heat transfer rate from a U-shaped channel, nf is the number of fins, σ is Stefan-Boltzmann constant, ε is surface emissivity, and t, tb, H, L and W are heat sink dimensions as shown in Figure 1. There has been extensive work to calculate
ch,r. However, no explicit analytical formulation is available to calculate
ch,r and its calculation usually requires the simultaneous solution of a set of three equations. Numerical results were obtained and presented in graphical forms as functions of channel surface emissivity and dimensions [1 � 3]. A simple and explicit analytical correlation for
ch,r is given here.
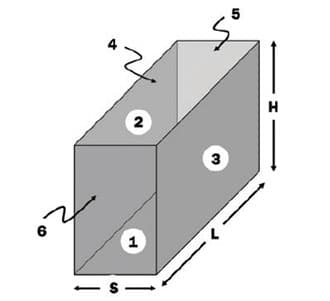 |
Figure 2. A typical channel created by two adjacent fins of a plat-fin heat sink.
A typical channel created by two adjacent fins of a plate-fin heat sink is shown in Figure 2. If the channel surface is diffuse and gray and the surrounding medium is very large and/or a black body, the net radiation heat transfer rate from this channel to its surrounding is
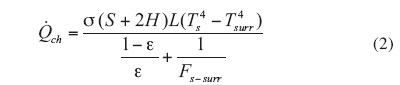 |
where Fs-surr, henceforth called channel view factor, is the total view factor between the walls and the base of the channel and its surrounding. It can be shown that the channel view factor is related to simpler view factors from the walls 1, 2 and 3 that constitute this channel to virtual walls 4, 5 and 6 that represent the surrounding for this channel [4].
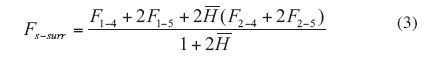 |
Here, = H/S is the normalized fin height and correlations for view factors F1-4, F1-5, F2-4 and F2-5 in terms of normalized fin height
and normalized fin length
= L/S were obtained [4] using the well -known view-factor correlations [5].
Although Equation 3 can be used to calculate channel view factor exactly, it involves complex expressions for view factors F1-4, F1-5, F2-4 and F2-5. A simple approximate correlation for channel view factor was developed by noting the limiting values of Fs-surr as and
approach zero and infinity;
 |
meets all conditions 4 � 7. The result is [4]
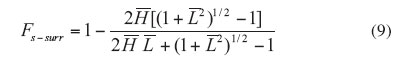 |
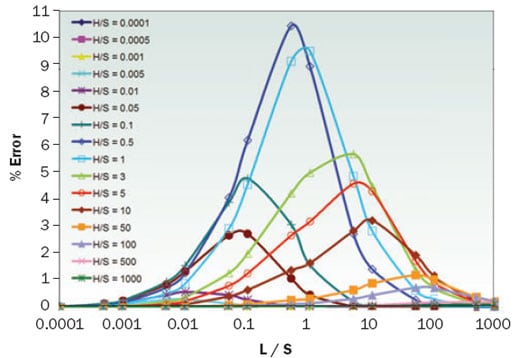 |
Figure 3. The error in approximate channel view factors calculated with Equation 9.
Figure 3 shows the percentage error associated with Equation 9 compared to the exact view factors calculated through Equation 3. It is seen that the approximate expression for channel view factor gives values within 11% of the exact values. However, this Figure shows that the error for most practical cases in which > 5 and
> 5 is less than 5%. The derivative of Equation 2 with respect to Fs-surr shows that
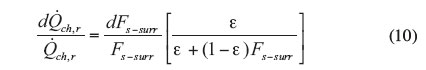 |
Equation 10 shows that the maximum error in calculated radiation heat transfer rate from a channel happens when the channel surface emissivity is equal to one and this error is exactly the same as the error associated with the error in channel view factor calculation.
Equation 1 assumes that the entire heat sink surface is at a uniform temperature Ts. A more accurate estimate of radiation heat transfer rate from this heat sink is obtained by using the well-known fin equations to account for temperature variation in the fins. First, a radiation heat transfer coefficient is defined as
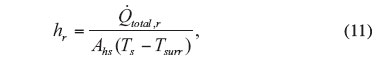 |
where
Ahs = (nf -1)SL + nf [t(L + 2H) + 2HL] + 2th(W + L) (12)
is the heat sink radiating surface area. Then, the radiation heat transfer rate from the heat sink is
where
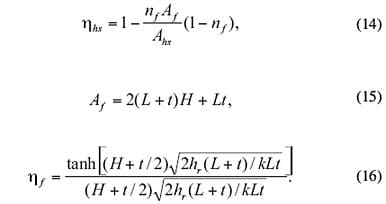 |
Equations 1, 2, 9 and 11 through 16 were used to calculate radiation heat transfer rate for a plate-fin extrusion aluminum heat sink and the results are compared with the data measured in vacuum by Rea and West [1] in Figure 4. The heat sink dimensions are L=127mm, H=38.3mm and W=92.2mm. It has nine 3.3mm-thick fins with fin spacing of S=7.8mm. The base thickness is tb=6.2mm.
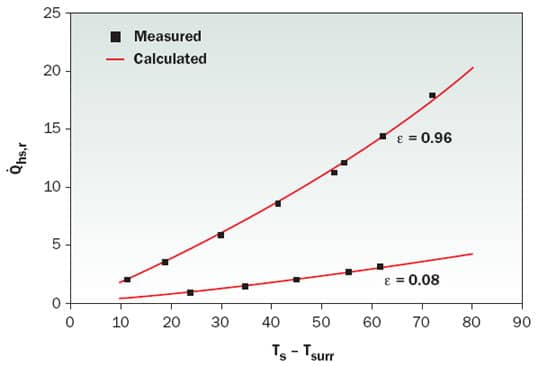 |
Figure 4. Measured and calculated radiation heat transfer rates from a plate-fin heat sink under vacuum conditions.
References
- Rea, S. and West, S., “Thermal Radiation from Finned Heat Sinks,” IEEE Transactions on Parts, Hybrids and Packaging, Vol. PHP-12, No. 2, June 1976, pp. 115 – 117.
- Ellison, N., ”Generalized Computations of the Gray Body Shape Factor for Thermal Radiation from a Rectangular U-Channel,” IEEE Transactions on Components, Hybrids, and Manufacturing Technology, Vol. CHMT-2, No. 4, December 1979, pp. 517 – 522.
- Bilitzky, A., “The Effect Of Geometry On Heat Transfer By Free Convection From A Fin Array,” MS Thesis, Dept. Of Mechanical Engineering, Ben-Gurion University of the Negev, Beer Sheva, Israel, 1986.
- Shabany, Y., “Radiation Heat Transfer from Plate-Fin Heat Sinks,” Proceedings of 24th Annual IEEE Semiconductor Thermal Measurement and Management Symposium (SemiTherm 24), March 16 � 20, 2008, San Jose, CA, Pages 133 � 137.
- Incropera, F., Dewitt D., Bergman, T. and Lavine A., “Fundamentals of Heat and Mass Transfer,” John Wiley and Sons, Hoboken, NJ, 2007.






