Cooling Electronics with Nanofluids: Laminar Convective Heat Transfer

Introduction

Numerous reports over the past ten years or so have described the potential for nanofluids (suspensions of nanoparticles in liquids) to be applied as heat transfer fluids, because of the enhanced thermal conductivity and convective heat transfer characteristics that have generally been observed. A number of review articles have been published on nanofluids [1 � 8], with most of the early emphasis placed on observed and predicted enhancements in the effective thermal conductivity. Recently, more attention has been paid to the convective heat transfer performance of nanofluids, due to the recognition that in practical applications nanofluids are likely to be used as heat transfer fluids in flowing systems, such as microchannel or minichannel heat sinks.

The purpose of this article is to describe some of the existing experimental data for convective heat transfer in nanofluids under laminar flow conditions (i.e., Re=UD_h/ν<2300, where Re is the Reynolds number, U the average velocity, D_h the hydraulic diameter, and ν the kinematic viscosity). The focus here is on laminar flow since liquid-cooled heat sinks are likely to be under such conditions. We discuss results for both fully developed and developing convective heat transfer, and briefly describe the existing state of models used for predicting convective heat transfer in nanofluids.

Experimental System for Measuring Convective Heat Transfer

Measuring the convective heat transfer of nanofluids is largely similar to comparable measurements on other liquids, with one possible exception: potential nanoparticle deposition. Nanofluids can be made stable against sedimentation through appropriate addition of surfactants or through the addition of acids or bases that increase the nanoparticle surface charge and thus help keep the nanoparticles separated from one another and in suspension. These additional chemicals, however, complicate the already complex nature of nanofluids and render the analysis of the experimental results more difficult. In our group, we have instead taken the approach to intentionally not add surfactants or any other chemicals to our nanofluids, even though we recognize that the resulting nanofluids will not be stable in the long term. Thus, we are forced to conduct our experiments shortly after the nanofluids are prepared.

For nanofluid preparation we follow the “two-step” process in which dry alumina nanopowder is purchased from a commercial vendor. The manufacturer’s stated diameter of the dry nanoparticles for our results reported here is 20 nm and 56 nm for some of the other results that we have taken from the literature. The desired amount is carefully weighed, added to the base liquid, and the resulting mixture is subject to ultrasonification for up to one hour in order to break up aggregates and disperse the nanoparticles. Here, we report results only for water-based nanofluids containing alumina nanoparticles, up to a volume fraction, φ, of 1 %. Many other types of nanofluids, however, have been tested in various labs around the world. These alumina/water nanofluids are meant to be representative of this large (and growing) body of nanofluids data.

A schematic diagram of our experimental system is provided in Figure 1. It was our intent to investigate only the laminar flow regime, and hence our test channel is a stainless steel tube with an inner diameter of 1.02 mm, and a wall thickness of 0.57 mm. The length of the tube, however, is 50 cm, which ensures that we maintain fully developed flow over a large portion of the tube length. The tube is heated by a polyimide-coated nichrome wire that is wrapped in a non-inductive fashion around the outside tube wall. “Non-inductively” means that the wire is doubled on itself, so that at any location on the tube there are opposing electric currents that effectively cancel the resulting magnetic fields. The system is first tested with pure water to confirm that both the heat transfer and the pressure drop measurements are accurate, after which the nanofluids are tested. In between nanofluid runs, the tube is thoroughly washed out with pure water to remove any deposited nanoparticles.

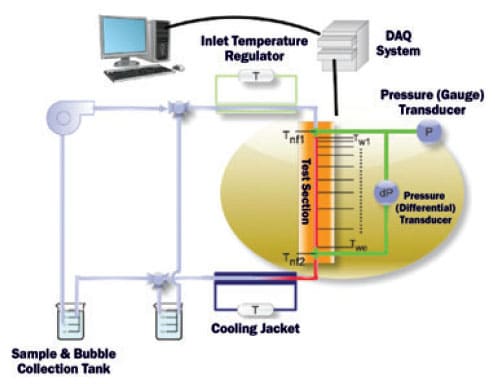Figure 1. Schematic representation of experimental system for measuring the laminar convective heat transfer for a nanofluid flowing in a single 50 cm long, 1.02 mm inner-diameter stainless steel tube.

Laminar Heat Transfer for Fully Developed Flow

All results reported here are for water-based nanofluids containing alumina nanoparticles. In order to make a meaningful comparison among various sets of data, both from our group and from others, we convert the dimensional data to nondimensional form by plotting the Nusselt number, Nu=hD_h/k, where k is the effective nanofluid thermal conductivity. Although one desires, where possible, to always speak in terms of dimensional (raw) data, it is difficult to plot multiple sets of raw data on a single graph and draw general conclusions. Thus, we resort to the time-honored tradition of first nondimensionalizing our data and those from other studies.

As considerable uncertainty in k can exist from batch to batch of nanofluids, one would ideally prefer measured k values to insert into the Nu relation. In the absence of measured k values, we instead compute k through the classical Hamilton-Crosser formula for spherical particles [9]:

where k_np and k_w are the nanoparticle and water thermal conductivity, and φ the nanoparticle volume fraction. This formula neglects any thermal contact resistance between the nanoparticles and the fluid, and the effects of aggregation, i.e., it assumes a well-dispersed nanofluid that may not exist in practice, but it should provide a reasonable estimate of k. It must be remarked, however, that for our own nanofluids in general we observe some aggregation as measured by a dynamic light scattering system [10]. Nevertheless, since we don’t know the exact extent of aggregation in all the data reported below, for consistency we apply equation 1 to all sets of data. Note that equation 1 has no explicit dependence of k on the nanoparticle diameter, so according to this relation the extent of aggregation would not change the value of k anyway. Other expressions for k, such as the Maxwell -Garnett model that includes the effect of thermal contact resistance between the nanoparticles and the base fluid, explicitly include the nanoparticle diameter [11], and more recent theories of nanofluid thermal conductivity emphasize percolation effects within the nanoparticle aggregates (see, e.g., [12, 13]).

For the values of n needed for Re, each experimental study cited in the following figures reported either their Re values or, in our case, the measured pressure drops across the test section from which we were able to determine ν. As expected the presence of the nanoparticles increases n over that for pure water. But, as discussed in [14], as long as this increase in ν is less than a factor of four greater than the corresponding increase in k, the use of nanofluids is still beneficial to heat transfer. We will leave the detailed report on our pressure drop measurements for a future publication.

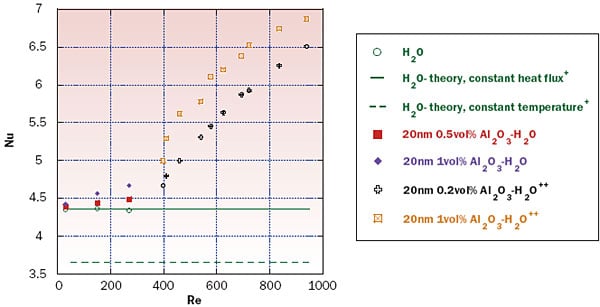
Figure 2 presents the results for fully developed flow for 22 < Re < 900, both from our own experiments (the lower range of Re) and from Heris et al. 2006 [15] (the higher values of Re). Nominally, all nanoparticles in both studies were 20 nm in diameter, although as mentioned above our own particle-sizing measurements have indicated that much larger aggregates can be present. The two classical theoretical curves are drawn for the case of pure water, with either a constant-temperature or a constant-heat-flux boundary. These results suggest that substantial enhancement in heat transfer coefficient, h, can be realized with nanofluids, albeit at the expense of greater viscosity and pressure drop. The mechanism(s) leading to this enhancement are not well understood at this time, and we will say more about this below when discussing the existing theoretical descriptions of convection in nanofluids.

Figure 2. Nusselt number vs Reynolds number in the fully developed region for water-based alumina nanofluids, where the classical theoretical results [16] indicate constant values of Nu. (+ = theoretical results, ⁺⁺ = Heris et al., 2006 [15]).

Laminar Heat Transfer for Developing Flow

For the relatively small heat sinks found in electronic packaging, such as those measuring only several centimeters on a side, the flow over much of the heat sink may be in the developing region. For laminar flow, the length of the developing region, also called the entrance region L_entrance, can be estimated from [17]

where D_i is the inner diameter of the tube and Pr the Prandtl number. For alumina-based nanofluids, Pr is given approximately as [14]

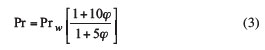where Pr_w is the Prandtl number of the base fluid, which here is liquid water. For φ = 1%, and assuming water at 25 �C, Pr = 6.43. Then taking D_i = 1.02 mm and Re = 500 gives L_entrance ≈ 16.4 cm. Thus, any heat sink smaller than L_entrance contains thermally developing flow rather than fully developed flow.

Figure 3 presents data from our own group and from Wen and Ding (2004) [18], for laminar thermally developing flow. Similar to the fully developed flow case in Figure 2, the nanofluids lead to substantially higher Nu compared to that for pure water. The results from [18] show markedly higher Nu than our results, but it should be pointed out that their Re numbers are also much higher. Furthermore, they stabilized their nanofluids with a dispersant that may also have had some effect.

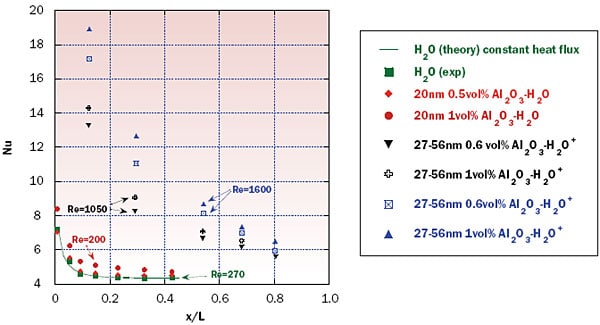Figure 3. Local Nusselt number values for water-based alumina nanofluids in the entrance (developing) region, where the theoretical curve is from [16] (⁺ = Wen & Ding, 2004 [18])

In a previous report [10] we argued that enhancements in the thermally developing region can probably be explained by well-known Prandtl (Pr) number effects, since Nu α Pr^1/2 and the Pr number for nanofluids increases with increasing nanoparticle volume fraction (equation 3). This explanation may suffice for the modest increases in Nu observed in our study, but likely do not explain the dramatic Nu enhancement observed in [18]. In another article Wen and Ding (2004) [19] noted that a nonuniform nanoparticle distribution over the tube cross-section could play an important role, and is featured in the theoretical descriptions of convection in nanofluids, as described next.

Theoretical Description of Convection in Nanofluids

Attempts to simulate the convective heat transfer performance of nanofluids have evolved from earlier homogeneous models to, more recently, two-component models in which the nanoparticles may not move at the same velocity as that of the local fluid (“slip”), and in which the nanoparticle distribution can be computed and taken into account [19 � 21]. All three of these studies conclude that the nanoparticle distribution plays an important role in determining the convective heat transfer of nanofluids, although much work remains to clarify the precise mechanism(s) that lead to the observed enhancements in h.

Arguably the most complete theoretical description of convection heat transfer in nanofluids is that given in Buongiorno (2006) [20]. He emphasizes how thermodiffusion and Brownian diffusion may cause a slip velocity between the nanoparticles and the fluid, and the importance of taking into account the nanoparticle distribution within the fluid.

Near a heated wall, for example, thermodiffusion would cause the nanoparticles to move away from the wall, leading to a reduced nanoparticle volume fraction near the wall. Such a reduced volume fraction, in turn, leads to a reduced viscosity and, to a lesser extent, a reduced near-wall thermal conductivity. For turbulent flow, this results in a reduction in the viscous sub-layer thickness and a consequent enhancement in turbulent convective heat transfer. For laminar flow, reducing the near-wall viscosity would extend the length of the developing region, but the effect on fully developed laminar convective heat transfer is less apparent.

Indeed, recent experiments by the same group [22] do not suggest any enhanced convective heat transfer for nanofluids, beyond what would be predicted using appropriate thermophysical property values for the investigated nanofluids. The results in [22], however, do not allow an explicit dependence of Nu on Re to be determined for fully developed flow, as given here in Figure 2. The unexpected increase in Nu as a function of Re exhibited in Figure 2 thus remains unexplained by existing theory.

Conclusions

Nanofluids are promising for application as heat transfer fluids in liquid-cooled electronic packaging, but experimental and theoretical work remains to clarify the heat transfer enhancement mechanisms. In particular, the local nanoparticle distribution appears to be key to understanding and optimizing the thermal performance of nanofluids. Possible degradation over time, such as through nanoparticle aggregation and/or sedimentation, also requires further study.

References

1. 1. Keblinski, P., Eastman, J.A., and Cahill, D.G., “Nanofluids for Thermal Transport,” Materials Today, June, 2005, pp. 36-44.
2. Phelan, P.E., Bhattacharya, P., and Prasher, R.S., “Nanofluids for Heat Transfer Applications,” Annual Reviews of Heat Transfer, Vol. 14, 2005, pp. 255 � 275.
3. Das, S.K., Choi, S.U.S., and Patel, H.W., “Heat Transfer in Nanofluids�A Review,” Heat Transfer Engineering, Vol. 27, 2006, pp. 3-19.
4. Trisaksri, V., and Wongwises, S., “Critical Review of Heat Transfer Characteristics of Nanofluids,” Renewable and Sustainable Energy Reviews, Vol. 11, 2007, pp. 512-523.
5. Wang, X.-Q., and Mujumdar, A.S., “Heat Transfer Characteristics of Nanofluids: A Review,” International Journal of Thermal Sciences, Vol. 46, 2007, pp. 1-19.
6. Daungthongsuk, W., and Wongwises, S., “A Critical Review of Convective Heat Transfer of Nanofluids,” Renewable and Sustainable Energy Reviews, Vol. 11, 2007, pp. 797-817.
7. Yu, W., France, D.M., Routbort, J.L., and Choi, S.U.S., “Review and Comparison of Nanofluid Thermal Conductivity and Heat Transfer Enhancements,” Heat Transfer Engineering, Vol. 29, 2008, pp. 432-460.
8. Murshed, S.M.S., Leong, K.C., and Yang, C., “Thermophysical and Electrokinetic Properties of Nanofluids�A Critical Review,” Applied Thermal Engineering, Vol. 28, 2008, pp. 2109-2125.
9. Hamilton, R.L., and Crosser, O.K., “Thermal Conductivity of Heterogeneous Two-Component Systems, Industrial and Engineering Chemistry Fundamentals,” Vol. 1, 1962, pp. 187-191.
10. Lai, W.Y., Phelan, P.E., Vinod, S., and Prasher, R.S., “Convective Heat Transfer for Water-Based Alumina Nanofluids in a Single 1.02-mm Tube,” 11th Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITHERM), May 28 � 31, 2008, Orlando, Florida, pp. 970 � 978.
11. Nan, C-W., Birringer, R., Clarke, D.R., and Gleiter, H., “Effective Thermal Conductivity of Particulate Composites with Interfacial Thermal Resistance,” Journal of Applied Physics, Vol. 81, 1997, pp. 6692�6699.
12. Prasher, R.S., Phelan, P.E., and Bhattacharya, P., “Effect of Aggregation Kinetics on the Thermal Conductivity of Nanoscale Colloidal Solutions (Nanofluid),” Nano Letters, Vol. 6, 2006, pp. 1529 � 1534.
13. Evans, W., Prasher, R.S., Fish, J., Meakin, P., Phelan, P.E., and Keblinski, P., “Effect of Aggregation and Interfacial Thermal Resistance on Thermal Conductivity of Nanocomposites and Colloidal Nanofluids,” International Journal of Heat and Mass Transfer, Vol. 51, 2008, pp. 1431-1438.
14. Prasher, R.S., Song, D., Wang, J., and Phelan, P.E., “Measurements of Nanofluid Viscosity and Its Implications for Thermal Applications,” Applied Physics Letters, Vol. 89, 2006, pp. 133108-1 � 133108-3.
15. Heris, S.Z., Etemad, S. Gh., and Esfahany, M.N., “Experimental Investigation of Oxide Nanofluids Laminar Flow Convective Heat Transfer,” International Communications in Heat and Mass Transfer, Vol.33, 2006, pp. 529-535.
16. Kays, W.M. and Crawford, M.E., Convective Heat and Mass Transfer, 1993, McGraw-Hill, Inc.
17. �engel, Y.A., Heat and Mass Transfer: A Practical Approach, 3rd Ed., McGraw-Hill, New York, 2007, pp. 455-458.
18. Wen, D. and Ding, Y., “Experimental Investigation into Convective Heat Transfer of Nanofluids at the Entrance Region under Laminar Flow Conditions,” Int. J. Heat Mass Transfer, Vol. 47, 2004, pp. 5181-5188.
19. Wen, D., and Ding, Y., “Effect of Particle Migration on Heat Transfer in Suspensions of Nanoparticles Flowing Through Minichannels,” Microfluidics and Nanofluidics, Vol. 1, 2005, pp. 183-189.
20. Buongiorno, J., “Convective Transport in Nanofluids,” Journal of Heat Transfer, Vol. 128, 2006, pp. 240-250.
21. Mirmasoumi, S., and Behzadmehr, A., “Numerical Study of Laminar Mixed Convection of a Nanofluid in a Horizontal Tube Using Two-Phase Mixture Model,” Applied Thermal Engineering, Vol. 28, 2008, pp. 717-727.
22. Rea, U., McKrell, T., Hu, L.-W., and Buongiorno, J., “Experimental Study of Laminar Convective Heat Transfer and Viscous Pressure Loss of Alumina-Water Nanofluid,” Proceedings of the Micro/Nanoscale Heat Transfer International Conference, Tainan, Taiwan, Jan 6-9, 2008, pp. 563-568.