Comparison Of Heat Transfer Rates Of Different Nanofluids On The Basis Of The Mouromtseff Number

Nanofluids are dispersions of nanometer-sized particles in a base fluid such as water, ethylene glycol or propylene glycol. In the last decade, nanofluids have attracted more attention as a new generation of coolants for various industrial and automotive applications. Use of high thermal conductivity metallic nanoparticles (e.g., copper, aluminum, silver, gold, etc.) effectively increases the thermal conductivity of such mixtures, thus enhancing their overall energy transport capability [1, 2]. Eastman et al. [3] showed a 40% increase in thermal conductivity with 0.3 volume percent of copper nanoparticles in ethylene glycol.

Electronic designs for application in innovative products that use higher powers in miniature systems are rapidly developing. This phenomenon has led to a dramatic increase in chip densities and power densities, as well as a continuous decrease in physical dimensions of electronic packages. Hence, thermal management continues to be one of the most critical areas in electronic product development. Similarly, advances in thermal management will significantly impact the cost, overall design, reliability, and performance of the next generation of weapons technology, which heavily uses microelectronic devices. In electronic cooling, as Azar [4] forecasted, heat fluxes of 1000 W/cm² will become a reality in the foreseeable future. Therefore, air may become impractical as a coolant; hence innovative liquid cooling ideas are receiving more attention.

In the world’s cold regions, such as Alaska, nanofluids may be very effective in such roles as household baseboard heating fluids and as coolants for automobiles and industries. Normally in these regions, 60:40 ethylene glycol/water or propylene glycol/water solutions are common choices due to their low freezing points. Therefore, for our analysis we investigated these fluids.

Simons [5] presented the effectiveness of various liquid coolants using the Mouromtseff number. The Mouromtseff number [6] is a Figure of Merit (FOM) for heat transfer fluids. Simons’ approach was further extended by Ellsworth [7]. A higher value of FOM for a fluid indicates better heat transfer characteristics. In electronic cooling, nanofluid flow through microchannels shows promise in removing high-density heat flux. In the present article we have extended the analysis of Simons to different nanofluids, which hold promise as a next generation liquid coolants.

The Mouromtseff number is given by

(1)where κ, ρ, c_p and μ are thermal conductivity, density, specific heat and dynamic viscosity of the fluid respectively. The exponents a, b, d, and e take on values appropriate to the heat transfer mode of interest and the corresponding heat transfer correlation. For a specific nanofluid, these thermo-physical properties depend on the nanoparticle material, base fluid and the nanoparticle volumetric concentration. Simons [5] showed the comparison of heat transfer rates for various typically used coolants with respect to water.

The thermal conductivity of a nanofluid is given by [3]

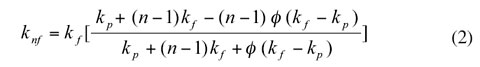where k_nf is the nanofluid thermal conductivity, k_f is the base fluid thermal conductivity, k_p is the bulk solid particle thermal conductivity, φ is the particle volume fraction, and n is an empirical scaling factor that takes into account how different particle shapes affect thermal conductivity. We used spherical nanoparticles in our experiments for which n = 3.

The effective density of nanofluids is given by [8]

where ρ_nf is the nanofluid density and ρ_s and ρ_f are the densities of the solid particles and base fluid, respectively.

The specific heat of nanofluids, c_pnf, can be calculated using the standard equation based on the volume fraction.

where c_ps is specific heat of solid particles and c_pf is specific heat of base fluid.

Various researchers have measured viscosities of several nanofluids. Kulkarni et al. [9] presented a correlation for the temperature dependency of viscosity for copper oxide nanoparticles in water using a Brookfield viscometer at different volume concentrations. The correlation is

where μ_s is the suspension viscosity in mPa-s (cP), T is the temperature in Kelvin, and A and B are polynomials which are functions of volumetric concentrations φ. These factors are given as

A = 20587φ² + 15857φ + 1078.3 with R² = 0.99

B = -107.12φ² + 53.548φ + 2.8715 with R² = 0.97

where φ is the volume fraction ranging from 0.05 to 0.15.

Researchers should note that each nanofluid exhibits different rheological properties; therefore different viscosity correlations for ethylene glycol/water and propylene glycol/water with CuO nanoparticles have been developed.

Qiang and Yimin [1] investigated the correlation for Nusselt number for a copper-water nanofluid. From experimental data reduction, the Nusselt number for laminar and turbulent flow is given by

μ_m is the mean velocity, d_p is average particle diameter (d_p < 100nm), α_nf is nanofluid diffusivity, and ν_nf is nanofluid kinematic viscosity.

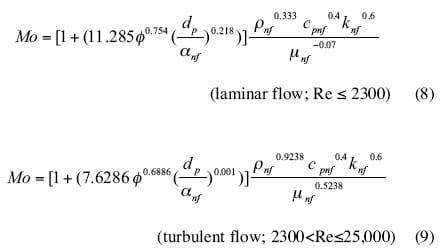
The Mouromtseff numbers derived from equations (6) and (7) for fully developed internal laminar and turbulent flow at a specific velocity of 1 m/s are given as

The following results (Figures 1, 2 and 3) are based on an average particle diameter of 50 nm and a mean velocity of 1 m/s for the same tube diameter. Further analyses for velocities of 5 m/s and 10 m/s and particle diameter of 100 nm indicate that similar trends are preserved for all nanofluids. The properties of various nanofluids used for further analysis are given in Table 1.

Table 1. Properties of Various Nanofluids with Varying Concentrations

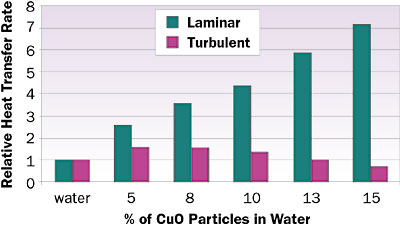
Figure 1. Comparative heat transfer rates (relative to water) for various concentrations of copper oxide (CuO) nanoparticles in water (at 20�C) for fully developed internal flow.

Figure 1 shows the relative heat transfer rate (Mo_nf/Mo_w) versus volume percent of copper oxide nanoparticles in water. For internal laminar flow, the nanofluids show a continuous increase in thermal performance with increasing particle concentration. However for turbulent flow, the relative heat transfer peaks at around 5% volume concentration and gradually diminishes after 8% volume concentration. This phenomenon is due to the increase in the viscosity of nanofluids at higher concentrations, which is inversely proportional to the Mo number (see Equation 9). This analysis suggests that for turbulent internal flow a 5 % volume concentration may be optimal. It must be emphasized that the heat transfer coefficient for turbulent flow is still much higher than that of laminar flow.

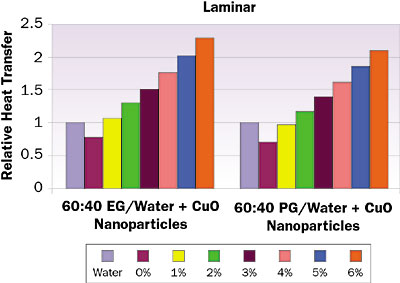Figure 2. Comparative heat transfer rates (relative to water) for various percentages of copper oxide (CuO) nanoparticles (at 20�C) for fully developed internal laminar flow.

Figure 2 shows the comparative heat transfer rate for 60:40 ethylene glycol/water and 60:40 propylene glycol/water with different concentrations of copper oxide nanoparticles for laminar flow. As in Figure 1, the relative heat transfer increases with the increase in nanoparticle concentration. Ethylene glycol performs better than propylene glycol (see Figure 2); this effect is due to the variation of several thermal properties. Ethylene glycol has higher thermal conductivity and density, and lower specific heat and viscosity than propylene glycol.

Figure 3. Comparative heat transfer rates (relative to water) for various percentages of copper oxide (CuO) nanoparticles (at 20�C) for fully developed internal turbulent flow.

Figure 3 shows the comparative heat transfer rate for 60:40 ethylene glycol/water and 60:40 propylene glycol/water with different concentrations of copper oxide nanoparticles for turbulent flow. Although these results show that pure water has a better FOM than these nanofluids under turbulent conditions, glycol solutions must be used in cold regions where fluid freezing is a serious problem. A concentration of 5% appears optimal for both of these nanofluids. These findings agree with the characteristics exhibited in Figure 1. It is also worth noting that the FOM of ethylene glycol is much better than propylene glycol.

Conclusion

In conclusion, for internal laminar flow, the FOM of water-based copper oxide nanofluids is much superior to pure water. For the same nanofluid, the optimal volume percentage appears to be 5% in internal turbulent flows. Ethylene glycol based nanofluids have a better FOM than propylene glycol based nanofluids.

Researchers are working on finding the compatibility of nanoparticles with pumps, valves and plumbing fittings. However, no definitive results have been published yet, because of the long-term experiments. It is generally thought that due to the small size of nanoparticles, wear on the surfaces will be minimal. We bought ready-to-use nanofluids. During the period of experiments conducted on the nanofluids, which lasted over several months, no agglomeration was observed. The cost of ready-to-use nanofluids is much higher than the traditional heat transfer fluids. For example, the authors recently purchased 500 gm (about 0.5 liter) of aluminum oxide nanofluid with a 50% concentration in water by weight for $120.00. By contrast, an equal volume of a traditional heat transfer fluid costs only $15.00 to $20.00.

References

1. L. Qiang. X. Yimin, “Convective Heat Transfer and Flow Characteristics of Cu-water Nanofluid,” Science in China (Series E), 45: 5, 408, 2002.
2. X. Yimin, L. Qiang, “Investigation on Convective Heat Transfer and Flow Features of Nanofluids,” ASME Journal of Heat Transfer, 125, 151, 2003.
3. J.A. Eastman, S.U.S. Choi, S. Li, W. Yu and L.J. Thompson, “Anomalously Increased Effective Thermal Conductivities of Ethylene Glycol Based Nanofluids Containing Copper Nanoparticles,” Applied Physics Letters, 78:6, 718, 2001.
4. Azar, K., “High Capacity or Not-do-it Up Front” Electronics Cooling, Vol. 12, No. 2, May 2006.
5. Simons, R., “Comparing Heat Transfer Rates of Liquid Coolants Using the Mouromtseff Number,” ElectronicsCooling, Vol. 12, No. 2, May 2006.
6. Bar-Cohen, A., Kraus, A., Advances in Thermal Modeling of Electronics Components and Systems, Vol. 2, ASME Press, 1990.
7. Ellswoth, M., “Comparing Liquid Coolants from Both a Thermal and Hydraulic Perspective,” Electronics Cooling, Vol. 12, No.3, August 2006.
8. Pak, B., Cho, Y., “Hydrodynamic and Heat Transfer Study of Dispersed Fluids with Submicron Metallic Oxide Particles,” Experimental Heat Transfer, Vol. 11, 1998, pp. 151-170.
9. Kulkarni, D., Das, D., Chukwu, G., “Temperature Dependent Rheological Property of Copper Oxide Nanoparticles Suspension (Nanofluid),” Journal of Nanoscience and Nanotechnology, Vol. 6, No.4, 2006.