Forced convention air cooled heat sinks and liquid cooled cold plates are quite pervasive in their use in electronics cooling applications. While there can be significant debate on whether to air or liquid cool a particular component, the approach a thermal engineer would adopt to design both components is essentially similar. Parallel plate fins are the most common geometry used to form the core structure of both devices. Simple hydraulic and thermal relationships from literature for plate fins and parallel plate ducts can be used for design. Often the first question that comes to mind before even starting a back of the envelope calculation for a heat sink or cold plate is: “What is the target volumetric flow rate and coolant pressure drop that we are designing towards?” The answer to this question is often determined from a high level system design that may estimate what the flow rate and pressure drop “budget” can be. It can also result from a choice of a fan that provides its user with a finite number of flow and pressure drop operating points. For air cooled heat sinks, another pertinent early question can be: “What is the volume available for this heat sink in the system?” This question may be less relevant for liquid cooled cold plates, because they are often extremely compact and small changes in their volume can usually be accommodated at the system level without too much difficulty.
It is often not obvious what geometry would satisfy target conditions for flow and pressure drop. This article will assume knowledge of target flow rate, pressure drop, and volume as design targets and will derive equations to allow thermal designers to design a heat sink or a cold plate to meet their needs. In this respect, this article differs from what has been previously published in this magazine [1], where the hydraulic and thermal performance of an assumed geometry was calculated. Although the previously presented calculations [1] can be and are often used, the methodology described herein could help designers converge more rapidly on geometries that match their specific needs.
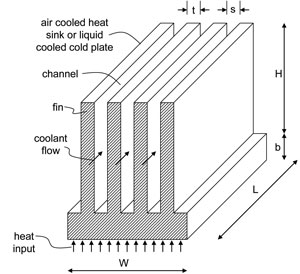
Figure 1 shows a schematic of an array of plate fins attached to a base with coolant (air or liquid) flow through the channels between the fins. The heat input, q, is assumed to be uniform for simplicity, although spreading in the base from a discrete heat source can be easily calculated using previous articles [2, 3]. Figure 1 shows the width, length, and height of the heat sink denoted as W, L, and H, respectively, and the fin thickness and channel spacing are represented by t and s, respectively. The thickness of the heat sink base is b. Flow bypass [4] is also not considered in this article. The analyses presented in this paper assumes the following:
• forced convection
• parallel plate heat sinks
• fully ducted flow
• fully developed laminar flow
• uniform heating of the heat sink base
• no entrance and exit effects
• equal number of fins and channels
• large aspect ratio for the channels
• high thermal conductivity fins
• uniform temperature on duct surface for Nusselt number estimation.
Neglecting the entrance (contraction) and exit (expansion) pressure losses, the pressure drop across a fully ducted heat sink can be assumed to be comprised of only the frictional component, and estimated by [5],
ΔP = f x (L/Dh) x (1/2) x (ρU2) (1)
where f, Dh, ρ and U are the Darcy friction factor, channel hydraulic diameter, fluid density, and channel flow velocity, respectively.
The Darcy friction factor is defined as a dimensionless pressure drop for internal flow [5], and for fully developed laminar flow between infinite parallel plate ducts, can be given by [6],
f = 96/Re (2)
where Re is the Reynolds number which is computed using,
Re = ρUDh/μ (3)
where μ is the fluid dynamic viscosity.
While the hydraulic diameter for ducts is defined as the ratio of four times the duct cross-sectional area to the duct perimeter, it can be approximated for high aspect ratio ducts to be,
Dh = 2s (4)
The channel velocity U is the ratio of the flow rate to the duct cross-sectional area, and is given by,
U = V/NHs (5)
where V is the coolant volumetric flow rate and N is the number of channels. The denominator in eq.(5) is the duct cross-sectional area.
Substituting eqs. (2)-(5) into eq.(1), we get, ΔP = (12μLV)/(s3NH) (6)
Since, we are assuming knowledge of the target design pressure drop to converge on the desired fin geometry, we can express eq.(6) as,
s = [(12μLV)/(ΔPNH)]1/3 (7)
After calculating the channel spacing that meets our needs, the fin thickness can be given by,
t = (W-Ns)/N (8)
Eq. (8) does assume that there are equal number of fins and channels which is a reasonable assumption when there are many fins and channels.
The dimensionless Nusselt number is often used to characterize heat transfer in channels, and is given by,
Nu = hchDh/kf (9)
where hch and kf are the channel heat transfer coefficient and fluid thermal conductivity, respectively.
Using the assumption of fully developed laminar flow in narrow ducts, the Nusselt number given by eq.(9) has been found to be 7.541 [6] for uniform temperature duct surfaces. Thus, by rearranging the terms in eq.(9), using eq.(4) and the value of 7.541 [6] for the Nusselt number, we can calculate the channel heat transfer coefficient as,
hch = 3.8 kf/s (10)
In order to calculate the thermal performance of this array, we need to calculate the fin efficiency, which can be given by [5],
η = tanh(mH)/(mH) (11)
where m is fin parameter which is calculated using,
m = (2hch/kt)0.5 (12)
where k is the thermal conductivity of the fin material.
The thermal resistance of the uniformly heated heat sink (or cold plate), R, can be formulated as,
R = Rconv + Rcal + Rbase (13)
where Rconv, Rcal, and Rbase are the convective, the caloric sensible coolant temperature rise, and the base 1-D conduction, components of the thermal resistance, respectively.
Eq. (13) can be further expanded to be expressed as,
R = 1/(hchNL(2ηH+s)) + 0.5/ρCpV + b/kLW (14)
where Cp is the fluid specific heat.
It should be noted that there exist other ways to construct a total thermal resistance as detailed in [7, 8] in which the heat sink surface is assumed to be at a uniform temperature. Under such an assumption, the caloric thermal resistance term (0.5/ρCpV) provided in eq.(14) would be replaced by a different term that accounts for a non-linear coolant temperature rise as it passes through a duct whose surface is at a uniform temperature. The term for the caloric thermal resistance in eq. (14) assumes that the uniform base heat flux would result in a linear coolant temperature along the length of the heat sink.
The important equations from the preceding analytical treatment that can be used by the thermal designer are eqs. (7), (8), (10), (11), and (14) which can lead to the calculation of thermal resistance for a heat sink design that would satisfy flow rate and pressure drop targets. In addition, the designer would have to specify a fin material (e.g. copper or aluminum), a coolant (e.g. air or water), a heat sink volume (L, W, H), the base thickness (b), and the number of channels (N). The last parameter, N, can be changed parametrically to yield multiple designs that satisfy the target constraints, and a design can be chosen based on the thermal resistance (R) as well as what fin thickness and channel spacing are manufacturable.

Table 1 shows results of such calculations for designing an air cooled aluminum heat sink that meets a target of 50 Pa at 0.0047 m3/s (10 cfm), for a fin array volume of 100 mm (L) by 100 mm (W) by 50 mm (H). For the results shown in Table 1, the base is assumed to be 5 mm. The channel number, N was varied from 20 to 80 to yield the results shown in Table 1, which result from the sequential use of eqs. (7), (8), (10), (11), and (14).
If the target heat load is 160 W at a heat sink base to inlet air temperature difference of 20 oC, then the target thermal resistance would be 0.125 oC/W. As seen from Table 1, the 50 fin design would yield such a design point. Such a heat sink would meet the target flow conditions and would comprise of 1.06 mm thick fins that are spaced 0.94 mm apart. Thus, both required cooling performance and heat sink manufacturability [9] would have to be considered in arriving at a desired design. If the manufacturable designs cannot provide the required cooling, then one or more of the target conditions may have to be changed. For example, the flow and pressure drop may need to be higher or the volume may be increased or a different fin material could be considered. Since the base thickness and volumetric flow rate is fixed for all the designs displayed in Table 1, they yield constant 1-D base conduction and caloric thermal resistances of 0.002 oC/W and 0.091 oC/W, respectively.
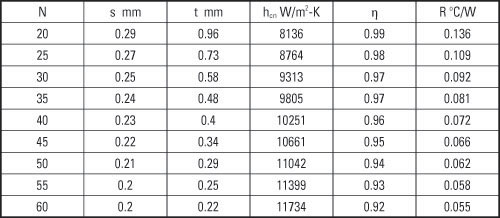
Table 2 shows a similar analyses as was discussed in the preceding text, but for a water cooled copper cold plate that is 25 mm (L) by 25 mm (W) by 1 mm (H) with a target flow rate of 6.308 x 10-6 m3/s (0.1 gpm) at 3447 Pa (0.5 psi). The base is assumed to be 2 mm. If the target heat load is 320 W with an available temperature excess of 20oC between the cold plate base and the inlet water, then the target thermal resistance would be 0.0625 oC/W. As can be seen from Table 2, a design using 50 fins with 0.29 mm thick fins spaced 0.21 mm apart would yield a thermal resistance of 0.0625 oC/W. Since the base thickness and volumetric flow rate is also fixed for all the designs displayed in Table 1, they yield constant 1-D base conduction and caloric thermal resistances of 0.008 oC/W and 0.019 oC/W, respectively.
It should be noted that the assumption of the 7.541 value for the fully developed laminar flow Nusselt number is good for very high aspect ratio (H/s) ducts. For smaller aspect ratios, such as 8 for example, this value is much lower (5.6) [5]. This effect can, if needed, be included into eq. (10) with an addition of an aspect ratio term, but has been left out for simplicity in this article. Also, the value of 7.5 is for a uniform temperature on the duct channel surface and the uniform heat flux boundary condition value is a bit higher (8.23) [5]. In reality, the boundary condition is neither a constant heat flux nor a constant temperature one.
Several other assumptions have been made in the calculations presented in this article. The objective has been to provide a rapid method to converge on some feasible geometries that address a target design point. For a specific design, it may be required to subsequently perform a full numerical analysis (CFD) or consider aspects such as entrance and exit pressure losses, the influence of the channel aspect ratio on the fully developed laminar Nusselt number, flow regime (laminar versus turbulent), the impact of developing flow, and the use of a precisely calculated hydraulic diameter. In addition to the heat sink calculation performed herein, one would of course need to calculate the bypass flow (if any), the spreading resistances (lid to heat sink base or at the chip hot spots) as well as the thermal resistance of all the thermal conduction layers between the heat sink base and the chip junction. In closing, even though this calculation corner provided numerical values to several digits, we should remember that the end result is only an estimate as mentioned in the first paragraph.
References
[1] R. Simons, “Estimating Parallel Plate-Fin Heat Sink Thermal Resistance,” Electronics Cooling, February, 2003.
[2] S. Lee, “Calculating Spreading Resistance in Heat Sinks,” Electronics Cooling, January, 1998.
[3] R. Simons, “Simple Formulas for Estimating Thermal Spreading Resistance,” Electronics Cooling, May, 2004.
[4] R. Simons, “Estimating the Effect of Flow Bypass on Parallel Plate- Fin Heat Sink Performance,” Electronics Cooling, February, 2004.
[5] F. P. Incropera, and D.P. Dewitt, “Introduction to Heat Transfer,” 2nd Edition, John Wiley and Sons, 1990.
[6] W. M. Rohsenow, J.P. Hartnett, and Y.I. Cho, “Handbook of Heat Transfer,” 3rd Edition, McGraw-Hill, 1998.
[7] R. Simons, “A Simple Thermal Resistance Model – Isoflux Versus Isothermal,” Electronics Cooling, February, 2006.
[8] R. Moffat, “Modeling Air-Cooled Heat Sinks As Heat Exchangers,” Electronics Cooling, February, 2008.
[9] M. Iyengar and A. Bar-Cohen, “Design for manufacturability of Forced Convection Air Cooled Fully Ducted Heat Sinks,” Electronics Cooling, August, 2007.






