Using commercially available finite element analysis (FEA) software is easier today than it has ever been. Software vendors have made great progress toward providing programs that are as easy to use as they are powerful. But, in doing so, software suppliers have created a perilous quagmire for unwary users. Some engineers and managers look upon commercially available FEA programs as automated tools for design. In fact, nothing could be further from reality than that simplistic view of today’s powerful programs. The engineer who plunges ahead, thinking that a few clicks of the left mouse button will solve all hisproblems, is certain to encounter some very nasty surprises.
Beware Discretization Errors
With the exception of a very few trivial cases, all finite element solutionsare wrong, and they are likely to be more wrong than you think. Surprised? Youshould not be. The finite element method is a numerical technique that providesapproximate solutions to the equations of calculus. All such approximatesolutions are wrong, to some extent. Therefore, the burden is on us to estimatejust how wrong our finite element solutions really are, by using a convergencestudy (which is also known as a mesh refinement study).
Performing a convergence study is quite simple. But before we plunge intothe details of convergence studies, we need to define an important term, ie.degrees of freedom (DOF). The DOF of a finite element model are unknowns, thecalculated quantities. For static structural problems in three dimensions, eachnode has three DOF, the three components of displacement. For heat transferproblems, each node has but one degree of freedom, ie. temperature. Increasingthe number of elements, all other factors being equal, results in a model withmore nodes and, therefore, more DOF.
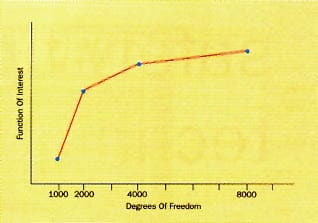
Doing a convergence study means that we treat number of DOF in our finiteelement model as an additional variable. We see how our function of interest isaffected by this additional variable. The easiest way to do this, of course, isto plot the function versus the number of DOF in the model. This is illustratedin Figure 1.
Figure 1: Illustration of a convergencestudy. Before the knee of the curve, a small change in the number of DOF yieldsa large change in the function. After the knee, even a large change in thenumber of DOF yields only a small change in the function.
The vertical axis in Figure 1 represents the function of interest. Thiscould be temperature, stress, voltage, or any measure of the performance of orproducts. The horizontal axis, in Figure 1, shows the number of DOF used foreach of the trial solutions. Here, we show only four trial solutions. Threeare an absolute minimum. Occasionally, five or more are needed.
Notice that the trial solutions are not evenly spaced. Instead, the numberof DOF has been doubled with successive trial solutions. This is necessary, toavoid generating trial solutions that are too close to each other. We shouldnot expect to see much difference between a trial solution obtained with 2000DOF and one obtained with 2500 DOF. If we were to use trial solutions soclosely spaced, we would probably fool
ourselves into thinking that we had obtained nearly converged solution. Wecan avoid this problem by spacing the trial solutions widely. Burnettrecommends at least doubling the number of DOF with successive trial solutions[1].
But why do a convergence study at all? Why not simply populate the modelwith, say, 10,000 elements or more, thus insuring an accurate solution? Supposewe do have a solution with a 0.01% error in it, but we don’t know that that isthe error. Can we have any confidence in our solution? A solution with even a0.01% error is worthless to us, if we do not know that that is the error. Onlyafter a convergence study, can we have any confidence in our results. But this,of course, is not the only reason for performing a convergence study. There isa second, more compelling reason.
We need to estimate the error in our earlier trial solutions, the ones thatwere obtained with fewer DOF. A single finite element solution can provide butone piece of data, one value for our function of interest. The information thatwe need is the answer to the question, “How do we design this product?” To deduce that answer, we need the data from tens of finite element solutions,not from just a single solution.
Our most accurate (converged) solution allows us to estimate the error inthe previous trial solutions. Since it is close to the exact solution, thedifferences between it and the earlier solutions are really estimates of theerrors in the earlier solutions. With those estimates, we can select the modelthat gives us the least accurate solution that is still acceptable. If we canlive with a 10% error in our finite element solution, then we want to use themodel that gave us that 10% error, because that model will give us the nextthirty or forty solutions economically, giving us the answer to the question “Howdo we design this product?” This is the greatest benefit provided byfinite element analysis.
Model the Physics
In the last section we talked about accuracy relative to the exactmathematical solution to the defined problem. But there is another kind ofaccuracy with which we must be concerned: accuracy relative to reality. By theestimate of one experienced analyst, (no, not me), 80% of all finite elementsolutions are gravely wrong, because the engineers doing the analyses makeserious modeling mistakes. Our failure to faithfully model the physics of aproblem can be devastating, and no convergence study can protect us from theoutcome. If we define the problem incorrectly, then we will never see thecorrect solution. Even worse, we are likely to generate and believe in aconverged solution to that erroneously defined problem.
Some years ago, while attending a conference, I watched as one presenterdiscussed how a finite element model and entire circuit of the board had beenused to supposedly improve the thermal performance of the board. I was quiteimpressed with the work until I asked the presenter how the thermal interfaceresistance between the components and the board had been modeled. As it turnedout, that resistance had not been taken into account.
The thermal resistance between two surfaces in contact is attributable tothe surface roughness of engineering materials. Try as we might to createperfectly smooth surfaces, we can never succeed. This is particularly true inproduction environment. Since thermal conduction is the result of interactionsbetween molecular neighbors, the conduction path between two solids isinterrupted at the contact surfaces. There, the two solids touch only where themicroscopic high-spots on their respective surfaces touch, as illustrated inFigure 2. Therefore, the cross-sectional area of the solid-to-solid conductionpath is greatly diminished. some thermal energy is indeed transferred from onesolid directly to the other solid, through the many contact points (actuallyminute contact areas). But much of the energy transfer is through the mediumthat occupies the interstitial voids, the valleys between the many peaks. Thatmedium is usually air, an excellent thermal insulator.
Figure 2: Due to the roughness ofengineering materials, the conduction path between two solid surfaces isinterrupted. Only a fraction of the transferred energy is conducted directlyfrom one solid to the other. Much of the heat transfer that takes place does sothrough the medium that occupies the voids between the two surfaces.
This insulating mechanism is the reason for the ubiquitous heat sinkcompound that is so popular among electrical engineers. The compound, athermally conductive gel, fills in the valleys. It displaces the thermallyinsulating air and provides a better conduction path between the two surfaces.
The thermal resistance between surfaces in contact is also a function of thenormal stress transmitted across the interface. When components are attachedwith screws to, say, a heat sink, the clamping force flattens many of the highspots on the contact surfaces and creates many additional contact areas, albeitmicroscopic ones. This decreases the thermal interface resistance.
The absence of a medium must also be considered. At altitudes in excess of24 km there remains very little air between the contact surfaces. The result isa drastic increase in the thermal interface resistance, as Steinberg reports[2].
One simple and easy way to account for the thermal interface resistancebetween two solids when defining a finite element model, is to include in themodel and additional, fictitious layer of solid finite elements. We can thenspecify the thermal conductivity of those elements in the three orthogonaldirections, so that we duplicate the physics that exist at the contact surfaces. In the direction perpendicular to the plane of contact, we specify a value ofthermal conductivity that will provide, on a macroscopic level, the thermalinterface resistance that we determine exists, according to empirical data. Inthe remaining two orthogonal directions, we specify a thermal conductivity thatis arbitrarily low. This forces our finite element model to permit heat flowonly through the plane of the fictitious elements, which are defined in a planeparallel to the plane of contact. Heat flow within the plane of the fictitiouselements is prevented by the arbitrarily low thermal conductivity that wespecify for the in-plane directions.
Is this an exact representation of the physics? Of course not. But it is aclose approximation, at least on a macroscopic level. However, unless we havemade some silly, arithmetic mistake in calculating our contrived thermalconductivity, any error introduced by this modeling technique is likely as smallas the discretization error.
In Conclusion
Finite element analysis is a very powerful tool with which to designproducts of superior quality. Like all tools, it can be used properly, or itcan be misused. The keys to using this tool successfully are to understand thenature of the calculations that the computer is doing and to pay attention tothe physics.