An introduction to thermoelectric coolers

Figure 1: Cross Section of a Typical TECouple

Introduction

Thermoelectric coolers are solid state heat pumps used in applications wheretemperature stabilization, temperature cycling, or cooling below ambient arerequired. There are many products using thermoelectric coolers, including CCDcameras (charge coupled device), laser diodes, microprocessors, blood analyzersand portable picnic coolers. This article discusses the theory behind thethermoelectric cooler, along with the thermal and electrical parametersinvolved.

How the Thermoelectric Works . . .

Thermoelectrics are based on the Peltier Effect, discovered in 1834, bywhich DC current applied across two dissimilar materials causes a temperaturedifferential. The Peltier Effect is one of the three thermoelectric effects,the other two are known as the Seebeck Effect and Thomson Effect. Whereas thelast two effects act on a single conductor, the Peltier Effect is a typicaljunction phenomenon. The three effects are connected to each other by a simplerelationship.

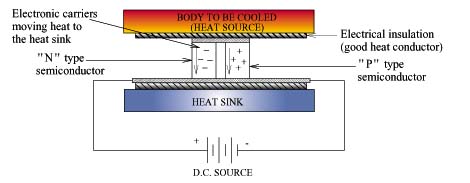
The typical thermoelectric module is manufactured using two thin ceramicwafers with a series of P and N doped bismuth-telluride semiconductor materialsandwiched between them. The ceramic material on both sides of thethermoelectric adds rigidity and the necessary electrical insulation. The Ntype material has an excess of electrons, while the P type material has adeficit of electrons. One P and one N make up a couple, as shown in Figure 1. The thermoelectric couples are electrically in series and thermally in parallel. A thermoelectric module can contain one to several hundred couples.

As the electrons move from the P type material to the N type materialthrough an electrical connector, the electrons jump to a higher energy stateabsorbing thermal energy (cold side). Continuing through the lattice ofmaterial, the electrons flow from the N type material to the P type materialthrough an electrical connector, dropping to a lower energy state and releasingenergy as heat to the heat sink (hot side).

Thermoelectrics can be used to heat and to cool, depending on the directionof the current. In an application requiring both heating and cooling, thedesign should focus on the cooling mode. Using a thermoelectric in the heatingmode is very efficient because all the internal heating (Joulian heat) and theload from the cold side is pumped to the hot side. This reduces the powerneeded to achieve the desired heating.

Thermal Parameters Needed

The appropriate thermoelectric for an application, depends on at least threeparameters. These parameters are the hot surface temperature (T_h),the cold surface temperature (T_c), and the heat load to be absorbedat the cold surface (Q_c).

The hot side of the thermoelectric is the side where heat is released whenDC power is applied. This side is attached to the heat sink. When using an aircooled heat sink (natural or forced convection), the hot side temperature can befound by using Equations 1 and 2.

(1)	Th = Tamb + (O) (Qh)
Where
	Th = The hot side temperature (°C).
	Tamb = The ambient temperature (°C).
	O = Thermal resistance of heat exchanger (°C/watt).
and
(2)	Qh = Qc + Pin
Where
	Qh = the heat released to the hot side of the thermoelectric(watts).
	Qc = the heat absorbed from the cold side (watts).
	Pin = the electrical input power to the thermoelectric (watts).

The thermal resistance of the heat sink causes a temperature rise aboveambient. If the thermal resistance of the heat sink is unknown, then estimatesof acceptable temperature rise above ambient are:

Natural Convection	20°C to 40°C
Forced Convection	10°C to 15°C
Liquid Cooling	2°C to 5°C (rise above the liquid coolant temperature)

The heat sink is a key component in the assembly. A heat sink that is toosmall means that the desired cold side temperature may not be obtained.

The cold side of the thermoelectric is the side that gets cold when DC poweris applied. This side may need to be colder than the desired temperature of thecooled object. This is especially true when the cold side is not in directcontact with the object, such as when cooling an enclosure.

The temperature difference across the thermoelectric (T) relates to T_hand T_c according to Equation 3.

(3) T = T_h– T_c

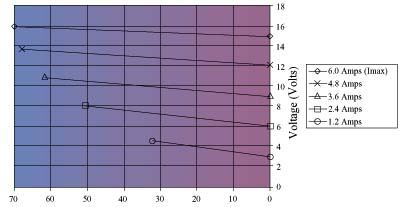
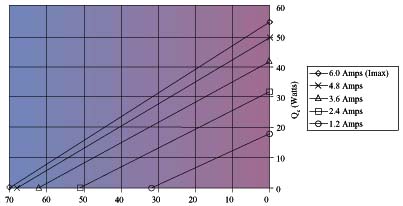
The thermoelectric performance curves in Figures 2 and 3 show therelationship between T andthe other parameters.

Estimating Q_c, the heat load in watts absorbed from the coldside is difficult, because all thermal loads in the design must be considered. Among these thermal loads are:

1. Active: I²R heat load from the electronic devices
   Any loadgenerated by a chemical reaction
2. Passive: Radiation (heat loss between two close objects with differenttemperatures)
   Convection (heat loss through the air, where the air has adifferent temperature than the object)
   Insulation Losses
   ConductionLosses (heat loss through leads, screws, etc.)
   Transient Load (time requiredto change the temperature of an object)

 

Powering the Thermoelectric

All thermoelectrics are rated for I_max, V_max, Q_max,and T_max, at aspecific value of T_h. Operating at or near the maximum power isrelatively inefficient due to internal heating (Joulian heat) at high power. Therefore, thermoelectrics generally operate within 25% to 80% of the maximumcurrent. The input power to the thermoelectric determines the hot sidetemperature and cooling capability at a given load.

As the thermoelectric operates, the current flowing through it has twoeffects: (1) the Peltier Effect (cooling) and (2) the Joulian Effect (heating). The Joulian Effect is proportional to the square of the current. Therefore, asthe current increases, the Joule heating dominates the Peltier cooling andcauses a loss in net cooling. This cut-off defines I_max for thethermoelectric.

For each device, Q_max is the maximum heat load that can beabsorbed by the cold side of the thermoelectric. This maximum occurs at I_max,V_max, and with T= 0°C. The T_maxvalue is the maximum temperature difference across the thermoelectric. Thismaximum occurs at I_max, V_max and with no load (Q_c= 0 watts). These values of Q_max andT_max are shownon the performance curve (Figure 3) as the end points of the I_maxline.

An Example

Suppose a designer has an application with an estimated heat load of 22watts, a forced convection type heat sink with a thermal resistance of 0.15°C/watt,an ambient temperature of 25°C, and an object that needs to be cooled to 5°C. The cold side of the thermoelectric will be in direct contact with the object.

The designer has a Melcor CP1.4-127-06L thermoelectric in the lab and needsto know if it is suitable for this application. The specifications for theCP1.4-127-06L are as follows (these specifications are at T_h = 25°C):

Imax = 6.0 amps

Qmax = 51.4 watts

Vmax = 15.4 volts

Tmax = 67°C

To determine if this thermoelectric is appropriate for this application, itmust be shown that the parametersT and Q_c arewithin the boundaries of the performance curves.

The parameter Tfollows directly from T_h and T_c. Since the cold side ofthe thermoelectric is in direct contact with the object being cooled, T_cis estimated to be 5°C. Assuming a 10°C rise above ambient for theforced convection type heat sink, T_h is estimated to be 35°C. Without knowing the power into the thermoelectric, an exact value of T_hcannot be found. Equation 3 gives the temperature difference across thethermoelectric:

T = T_h – T_c= 35°C – 5°C = 30°C

Figures 2 and 3 show performance curves for the CP1.4-127-06L at a hot sidetemperature of 35°C. Referring to Figure 3, the intersection of Q_cand T show that thisthermoelectric can pump 22 watts of heat at aT of 30°C with aninput current of 3.6 amps.

Performance Curve (T vs. Voltage)

T( °C)

Figure 2: Melcor CP1.4-127-06L, ^T vs.Voltage

Performance Curve (T vs. Qc)

T( °C)

Figure 3: Melcor CP1.4-127-06L, ^T vs. Qc

These values are based on the estimate T_h = 35°C. Once thepower into the thermoelectric is determined, Equations 1 and 2 can be used tosolve for T_h and to determine whether the original estimate of T_hwas appropriate.

The input power to the thermoelectric, Pin, is the product of the currentand the voltage. Using the 3.6 amp line in Figure 2 for the current, the inputvoltage corresponding to T= 30°C is approximately 10 volts.

Using Equations 1 and 2, T_h can now be calculated.

	Th = Tamb + (O) (Qh)
	where Tamb = 25°C O = 0.15°C/watt
	Qh = Qc + Pin = 22 watts + ((3.6 amps)* (10 volts)) = 22 watts + 36 watts = 58 watts
therefore	Th = 25°C + (0.15°C / watt) (58 watts)
	= 25°C + 8.7°C = 33.7°C

The calculated T_h is close enough to the original estimate of T_h,to conclude that the CP1.4-127-06L thermoelectric will work in the givenapplication. If an exact solution needs to be known, the process of solving forT_h mathematically can be repeated until the value of T_hdoes not change.

Other Parameters to Consider

The material used for the assembly components deserves careful thought. Theheat sink and cold side mounting surface should be made out of materials thathave a high thermal conductivity (i.e., copper or aluminum) to promote heattransfer. However, insulation and assembly hardware should be made of materialsthat have low thermal conductivity (i.e., polyurethane foam and stainless steel)to reduce heat loss.

Environmental concerns such as humidity and condensation on the cold sidecan be alleviated by using proper sealing methods. A perimeter seal (Figure 4)protects the couples from contact with water or gases, eliminating corrosion andthermal and electrical shorts that can damage the thermoelectric module.

Figure 4: Typical thermoelectric from Melcorwith a perimeter seal

The importance of other factors, such as the thermoelectric’s footprint, itsheight, its cost, the available power supply and type of heat sink, varyaccording to the application.

Single Stage vs. Multistage

Given the hot side temperature, the cold side temperature and the heat load,a suitable thermoelectric can be chosen. IfT across thethermoelectric is less than 55°C, then a single stage thermoelectric issufficient. The theoretical maximum temperature difference for a single stagethermoelectric is between 65°C and 70°C.

If T is greater than55°C, then a multistage thermoelectric should be considered. A multistagethermoelectric achieves a highT by stacking as many assix or seven single stage thermoelectrics on top of each other.

Summary

Although there is a variety of applications that use thermoelectric devices,all of them are based on the same principle. When designing a thermoelectricapplication, it is important that all of the relevant electrical and thermalparameters be incorporated into the design process. Once these factors areconsidered, a suitable thermoelectric device can be selected based on theguidelines presented in this article.

Sara Godfrey
Melcor Corporation, 1040 Spruce Street
Trenton, NJ08648, USA
Tel: +1 (609) 393 4178
Fax: +1 (609) 393 9461
Email:tecooler@melcor.com

References

1. Levine, M.A., Solid State Cooling withThermoelectrics, Electronic Packaging & Production, Nov. 1989.
2. Melcor Corporation, Thermoelectric Handbook, Sept., 1995.
3. Rowe, D. M., CRC Handbook of Thermoelectrics, CRC Press, Inc., 1995.
4. Smythe, Robert, Thermoelectric coolers take the heat out of today’s hotchips, Electronic Products, Aug. 1995.