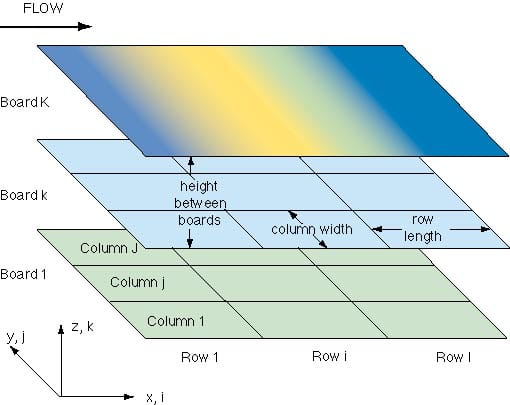
Figure 1: Basic discretization of parallel board arrangement
Introduction
While electronic systems thermal managementgrows in complexity, the challenge of integrating thermal constraints intothe product design process remains constant. The evolution of compactcomponent models highlights the need to predict integrated systemperformance on the basis of the individual component characterization[1]. The proper manner of treatinginteractions, such as formulating interfacing boundary conditions, remainsthe source of controversy [2]. Thepurpose of this article is to remind the readership of the utility ofthermal network models to help understand component to component thermalinteractions, especially at the board level. The approaches to bediscussed are most easily applied to air-cooled applications involving oneor more circuit boards. The models described can be the basis fordeveloping “home grown” software. In many instances, this is auseful strategy because the analyst has full control of the model and thedata. These approaches are also used, to various degrees, in commercialsoftware packages.
Modeling approach
Integrated thermal network models areformulated by combining two established analysis techniques – thermalnetworks to describe component level heat transfer and integral momentumand thermal energy balances to provide conjugate thermal linkages. Theterm integral implies conservation on a control volume or averaged basis.This approach is analogous to the integration of compact component modelsinto system-level CFD codes (e.g. the DELPHI project [3]).Consider the basic problem geometry illustrated in Figure 1. Individual circuit boards, identified by the index “k”, are mounted inparallel. These boards can be divided into streamwise (i) and lateral (j)sections. A “section” may correspond to the region in thevicinity of a component. Regions communicate thermally by conduction,convection and radiation.
There are three structural parts in an integrated thermal network model – a regional thermal modeling “unit” or TMU, a methodology forintegrating TMU-to-TMU thermal communication, and a computational strategysince closed form solutions of the combined equation sets can not beobtained.
Thermal Modeling Unit – TMU: The over-riding requirement fordeveloping a useful TMU is that it describes the heat transfer to theanalyst’s satisfaction and that it provides sufficient interfaceparameters. The following TMU uses a single chip, one component unit forillustration. Other TMU’s can be developed depending upon the componenttechnology (e.g. MCM) or mounting modality (e.g. surface mount).
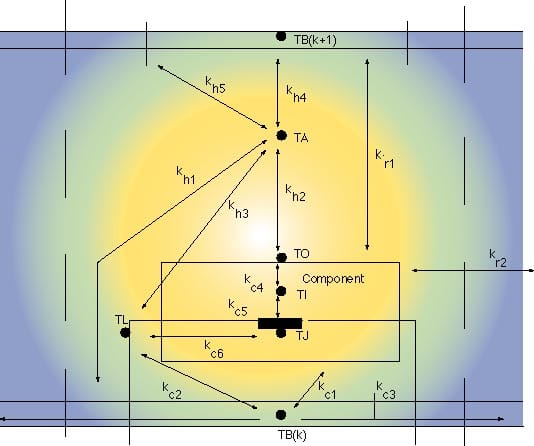
Consider Fig. 2. Each TMU consists of a component, board and associated coolant region. Several simultaneous network equations describe the TMU.The number of these equations will vary with the complexity of the model.While forced, free or mixed convection can be modeled, a “dominant” flow direction is required since marching numerical solutions are employed to achieve flow solution convergence. Lateral “cross-flows”should be included. Inter-unit conduction (c) as well as radiative (r)exchanges are assumed to be dominated by interactions with the nearestneighboring units. Radiative exchanges should also include “board toboard” transfer. Convective exchanges (h) describe surface to local,not room, ambient heat transfer.
Figure 2: Illustration of the Inter- and Intra-TMU HeatTransport Conductances
The outside-of-component exchanges illustrated in Fig. 2 are fairlyuniversal. While internal component models will vary depending upon thecomponent being modeled, experience shows that roughly two identifiable “internal” component temperatures (at least one per junction or chip) and four or five internal conduction paths are usually sufficient to resolve thedominant thermal characteristics of most packages.
The TMU includes characteristic temperatures which define its thermalstate and which provide the interfacing parameters among units. In thecase illustrated, six temperatures – TA, TB, TI, TO, TJ and TL – areidentified. The number of characterizing temperatures defines the numberof simultaneous nodal equations which need to be solved per TMU. Severalthermal conductances (‘s), defined schematically in Fig. 2, are used in Eqs. (1)-(6).
The temperatures, conductances and other parameters (e.g. ) in Eqs.(1)-(6) are for TMU “i,j,k” unless otherwise noted. For example,TA is actually TAijk while TBk+1 is TBijk+1.In other words, the “k+1” subscript implies the TMU directlyabove TMU “ijk”. The term “neighbors” implies theclosest four longitudinal (i) and lateral (j) TMU’s. is F volumetric flowrate (e.g. m3/sec) and x representsthe “cross-flow” convective energy transport using a donor celllogic, that is, the magnitude of the cross-flow rate and relevant airtemperatures depend upon the direction of the cross-flow across lateralboundaries (j±1). The heat transport conductances are defined usingthe following general prescriptions:
| Equation 7 |
where lc is the appropriateconduction thickness, kc is theappropriate thermal conductivity, Ac,Ah and Ar are the appropriate heat transfer areas, h is the appropriate convection coefficient and hr is the effective radiative heat transfer coefficient.The goal of these models is to get useful answers. One must keep in mind that these are performance models, that is, models that should evolve onthe basis of experience. Model tuning is not only allowed, it is required!The most important capability is to be able to vary the formulation of theconductances. While achieving accurate estimates for these parameters mayappear to be a daunting task, the fact of the matter is that conduction,convection and radiation conductances available in basic heat transfertexts can be used with great success. For example, conductancec4 might be represented by a lumped parameterspreading resistance based upon package geometry, conductance
h3 might be estimated by modeling the leads ascylinders or bars in a cross-flow, while radiative conductance
r2 might be estimated using the method of “crossedstrings” to compute the radiative view factors directly from thecomponent size and placement [4]. Anexcellent illustration of this strategy is the work of Guenin et al. intheir analysis of ball grid array packages [5].TMU-to-TMU thermal transport: Equation (1) is an integral formof a thermal energy balance for the TMU. It equates the convectivetransfer of heat from the various surfaces in the modeling unit(component, board, leads, etc.) to the change in the local ambient airtemperature based upon the flow rates in and out of the control volume. Assuch, local inter-TMU flow rates are needed.
The volumetric flow through a computational unit in the dominant flowdirection can be estimated based upon the following integral form of amomentum balance
| Equation 8 |
The D’s are hydraulic resistance factors and Hbuoy is the relative height of a TMU. The two contributions to the flowresistance (left hand side of Eq. (8)) are due to form (fo) and friction(fr). Frictional contributions can be computed using the local streamwisevelocity, an estimate of the local boundary layer thickness (laminar orturbulent) and the viscosity of the coolant, i.e. air. The two drivingforces (right hand side of Eq. (8)) are assumed to be either an imposedpressure gradient (e.g. fan) and/or a net buoyancy head. Each TMU willhave its own version of Eq. (8). These simultaneous equations, one perTMU, should be solved by applying the constraint that the pressure alongany lateral line (constant j index) be equal. Once the flow in thepredominant direction is computed, the “cross-flow”contributions can be computed by imposing conservation of mass. Thesecross-flows (magnitude and direction) are used to evaluate the terms in Eq. (1).Computational strategy: The equation sets are best solved as an iterative calculation. While spreadsheets or mathematical analysissoftware (e.g. MathCAD®, MATLAB®, etc.) can be used, it is the author’sexperience that a program written in a scientific programming language ismore versatile.A basic computational logic is as follows:
Computational logic
Initialization
| i) | Input physical data and simulation control (convergence criteria, dP’s, etc.) |
| ii) | Estimate volumetric flows per board including cross-flows – Eq. (8) |
| iii) | Estimate initial values for conductances (k’s) – Eq. (7) |
Iteration
| iv) | Solve Eqs. (1)-(6) for each unit sequentially. |
| v) | If natural convection is to be considered, recompute flows using new estimates for local air temperatures. |
| vi) | Check convergence of board-level energy and momentum balances. |
| vii) | If tolerances met, move to Output Processing. If tolerances not met, recalculate frictional loss coefficients and flows, conductances – Eq. (7) and loop back to step iv. |
Output Processing
| viii) | Create data files as needed for text-based and graphical output |
| ix) | Create restart data files, if any. |
The convergence identified in Step vi) should check both momentum andenergy conservation. As to the former, the total pressure change across aboard in the dominant flow direction should equal the sum of the pressurechanges imposed by a fan, or as an input value, added to the net change inthe buoyancy head. As a convergence check for energy conservation, asystem-level energy balance (see Eq. (9)) should equate the increase inthermal energy of the total flow (i.e. all boards) plus any heat losses tothe true ambient (cabinet to room air) heat transfer, to the total powerdissipated on all boards.
| Equation 9 |
where Too is the room ambienttemperature.
Demonstration
The following example is meant to illustratethe type of problem that can be solved. Consider the singlemulti-component board illustrated in Fig. 3. The air flowed over and belowthe board in the direction noted in the figure. The shaded components arepower supplies which were modeled as single material, conductive blocks(no leads) dissipating 10, 7 and 4 Watts (ordered in stream-wisedirection), respectively. The numbered components (Nos. 1 through 11) were leaded, three-layer components with bottom mounted dies.
Figure 3: Multi-component, non-uniform array test boardschematic (air flow above & below board)
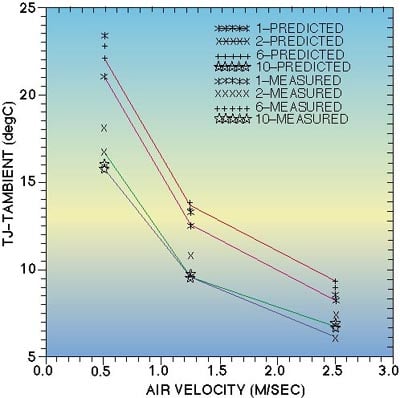
Figure 4 is a comparison of computed and measured component temperatures as a function of approach velocity for a series of tests in which all 11components were powered at 2 Watts. These results were obtained after themodeling parameters (e.g. convection conductances) were tuned to best meetthe experimental measurements taken at 1.25 m/sec approach velocity. Thisillustration shows that once a model is calibrated using one or a few datapoints, it can be used to provide thermal characterization data over awide parameter space.
Figure 4: Comparison of measured and predicted componentstemperatures as a function of air approach velocity (T-AMBIENT=RoomAmbient)
Closure
These simple, engineering models still have a place in electronic thermal management. Admittedly, their initial developmentwill take some time. However, once in hand, they can be used to estimateperformance as a function of system-level design variation variations.They are useful for interpreting and reducing the number ofcharacterization measurements. Finally, since they are based onstraightforward, albeit approximate, physics-based models, they are useful for checking the sanity of more complex CFD calculations.
References
| 1. | A. Bar-Cohen and W.B. Krueger, “Thermal Characterization of Chip Packages – Evolutionary Development of Compact Models”, Thirteenth Annual Semiconductor Thermal Measurement and Management Symposium – SEMITHERM XIII, Austin, TX, January 28-30, 1997 IEEE, pp. 180-197. |
| 2. | C.J.M. Lasance, “Thermal Resistance: An Oxymoron?”, Electronics Cooling, Vol. 3, No.2, May 1997, pp. 20-22. |
| 3. | H.I. Rosten et al., “Final Report to SEMITHERM XIII on the European-Funded Project DELPHI – The DEvelopment of Libraries and PHysical Models for an Integrated design environment”, Thirteenth Annual Semiconductor Thermal Measurement and Management Symposium – SEMITHERM XIII Austin, TX, January 28-30, 1997, IEEE, pp. 73-91. |
| 4. | F. Kreith and M.S. Bohn, Principles of Heat Transfer, Fifth Edition (Revised Printing), PWS Publishing, 1997, pp. 593-594. |
| 5. | B.M. Guenin, R.C. Marrs and R.J. Molnar, “Analysis of a Thermally Enhanced Ball Grid Array Package”, IEEE Transactions on Components, Manufacturing, and Packaging Technology – Part A, Vol. 18, No. 4, 1995, pp. 749-757. |