Introduction
High altitude air cooling has always been somewhat of a mystery to the uninformed. The first reaction to the situation is that there is just not enough air at altitudes greater than six kilometers (20,000 ft). At times this may be true, but many things can be done to improve the cooling and obtain an acceptable design. The most important thing to remember when designing for high altitude air cooling is to look at the numbers, do the calculations and then decide whether it can be done. Many people will be surprised that high altitude air cooling can be done without adding the great complexity of a pressurized system or even liquid cooling. This paper describes fan cooling at high altitude although much of the information can be used with any forced air cooling system.
Nomenclature
| A | general loss factor |
| A1 | minor loss factor |
| A2 | viscous loss factor |
| Ax | cross sectional area of fluid passage (m2) |
| cp | specific heat (J/kg°C) |
| D, Dh | diameter, hydraulic diameter (m) |
| f | Darcy friction factor |
| h | film coefficient (W/m2°C) |
| K | head loss coefficient |
| k | thermal conductivity (W/m°C) |
| L | length of fluid passage (m) |
| µ | dynamic viscosity (poise) |
| mass flow rate (kg/s) | |
| NNu | Nusselt Number |
| NRe | Reynolds Number |
| P | total fluid pressure (kPa) |
| Q | volume flow rate (m3/s) |
| heat rate (W) | |
| fluid density (kg/m3) | |
| density ratio | |
| T | temperature (°C) |
| v | velocity (m/s) |
Air properties vs altitude
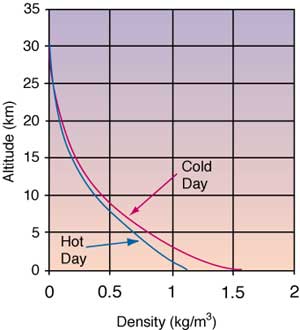
The temperature of the air at high altitude is very important to the design. In most hot day cases the air temperature decreases with altitude. The lower inlet temperature to the unit reduces the flow rate required. Typically the reduction in temperature only occurs up to approximately twelve kilometers (40,000 ft). On most cold days the temperature actually increases with altitude in the first three kilometers then the temperature begins to decrease. Cold days are not of great concern because the hot day defines the design point for worst case cooling conditions.
The pressure at different altitudes is what drives the density of the air because as the pressure decreases with altitude so does the air density. For all practical purposes above twenty one kilometers (70,000 ft) the air pressure is so low that almost no air is available for cooling.
The density of the air is a very important parameter in any air cooling design and especially important for high altitude air cooling. As the density of the air decreases with altitude as shown in Figure 1 the volumetric flow (m3/s) needed to cool the unit must increase. This means that a fan with a higher volumetric flow is needed.
Figure 1: Altitude vs. density
System pressure drop
Minor and viscous loss characteristics
The pressure drop in air passages can be characterized as being caused by one of two factors: minor loss,
K ½ V2
and the viscous loss,
(fl / D )½ V2
Combining these two losses into one equation gives
P = K ½
V 2 + (4 fl / D) ½
V 2
A series of cross sections making up a system having individual loss coefficients, ki and cross sections, Axi can be combined into one minor loss factor, A1 while the individual fl / D terms can be combined into one viscous loss factor, resulting in the system pressure drop
P = A1
Q2+ A2µ 2-n
n-1Qn
where n varies from 1 to 2.
Under atmospheric conditions the variation in the air viscosity is small. For most forced-air-cooled systems the flow in the internal passages is turbulent and so the exponent, n tends to vary from 1.78 to 2. As a result the viscosity term µ 2-n varies by only as much as 8%. So for forced-air-cooled systems at atmospheric conditions the effect of the variation of viscosity on air pressure drop can be neglected. The minor loss, A1 Q2 is identical in form to a special case of the viscous loss, A2
n-1Qn when n=2.
By summing up series and parallel combinations of cross sections making up a system the minor and viscous loss characteristics can be combined into one general loss factor, A and exponent, n where P = A
n-1Qn and n varies from 1.78 to 2. A more convenient form is
P = A
n where
is the density ratio is given by
P = A
n where
is the density ratio is given by
=
alt/
sea level.
Variation with density
As the density decreases with altitude pressure drop decreases. If the volume flow rate, Q is held constant the pressure drop decreases as n-1 which for most systems is quite close to linear. If the mass flow rate,
is held constant the pressure drop decreases linearly with density. Figure 2 shows an example of the variation in system pressure drop with density.
Figure 2: Pressure drop variation with density
Conventional fans
In a conventional fan the blades run at a constant speed. In a standard fan curve as shown in Figure 3 the speed is nearly constant throughout the entire fan curve even though the pressure and flow rate changes.
Figure 3: Non-slip fan curve
These changes are due to the blade design running at a certain speed. Pressure drop and flow rate curves vary for a conventional fan according to the air density. The volumetric flow rate for a given fan is constant, while the pressure output by this fan is drastically different at different altitudes. This can be seen by the two fan laws shown below.
As stated fan size and speed is constant, so that these equations reduce to:
The pressure output of the fan is directly proportional to the density of the air. Although the volumetric flow rate is constant the mass flow rate will drop with density.
“Slip” fans
A slip fan is very different from a conventional fan. A slip fan allows the blades to slip or run at different speeds from the motor driving the fan. This somewhat simple idea produces a fan that can work under many different altitudes and changing density conditions. As shown in Figure 4 the pressure flow rate curves at different altitudes are more consistent than a conventional or non-slip fan.
Figure 4: Slip fan output at altitude
Slip fans usually give curves showing the mass flow rate of the fan at different densities as shown in Figure 5.
Figure 5: Slip fan curve density vs. mass flow rate
The mass flow is the most important factor in the cooling design, because the more mass flow that can be pushed through the system the lower the air temperature rise from inlet to outlet. Even at very low densities a slip fan still produces a reasonable mass flow rate. For example the mass flow at a sea level density of 1.12 kg/m3 is 0.053 kg/s and at a twenty-one kilometers density of 0.064 kg/m3 the mass flow is 0.0075 kg/s. The reduction in density is seventeen times lower while the mass flow rate is only reduced by seven times.
System-fan integration
General considerations: When selecting a fan to cool forced-cooled equipment it is important to match the fan supply curve to the system pressure drop curve. The point at which the curves cross is the operating point and determines the flow rate and pressure drop. The selected operating point must be a stable and obtainable point with sufficient flow rate to provide the cooling required (both advection and convection).
Fan selection for high altitude operation:
When selecting a fan to operate at a high altitude the effect of low density and temperature on pressure drop, advection and heat transfer must be considered. Once the mass flow rate requirement at altitude alt is established the volume flow rate required is simply
Qalt = alt /
alt
How the volume flow rate of the fan varies with density depends on whether the fan runs at a constant speed (conventional) or slips.
Conventional fans:
A conventional fan as shown in Figure 6 runs at a constant speed. When a conventional fan supplies air to a system, as shown in Figure 6 the resulting operating point varies with density.
Figure 6: Conventional fan/system operation
As the density decreases the pressure drop decreases and the volume flow rate decreases slightly. The amount the flow decreases is a function of the exponent in the system resistance,
P = A
n-1Q n.
The exponent, n varies from 1.78 to 2. When the exponent approaches 2 the fan pressure and the system pressure both decrease linearly with density and the volume flow rate remains constant. When the exponent falls below 2, the system resistance decreases less than the fan supply pressure decreases. So in general the volume flow rate decreases as much as
/
n-1 =
2-n
depending on how the operating point moves along the fan curve.
“Slip” fans: A slip fan as shown in Figure 4 does not run at a constant speed. As the load on the fan increases it slows. When a slip fan supplies air to a system, as shown in Figure 7 the resulting operating point varies with density.
Figure 7: slip fan/system operation
As the density decreases the pressure drop decreases and the volume flow rate increases. The amount the flow increases is a function of the exponent in the system resistance,
P = A
n-1Q n
and the amount the fan speeds up. Slip fans typically speed up to a synchronous speed and then run constantly at that speed. As a result the operating volumetric flow rate increases as density decreases up to the fans maximum speed then decreases slightly similar to a conventional fan operation as shown in Figure 6.
Heat transfer
Advection: The process of carrying the heat in the sensible heat of the fluid to another location is called advection. Advection is proportional to the volume flow rate, Q, the density, , and the specific heat,cp of the fluid.
For fan cooled equipment at altitude the advection of heat decreases dramatically as both volume flow rate and density decrease with altitude. As a result the inlet to outlet temperature rise increases with altitude. Fortunately the inlet air temperature decreases with altitude up to nine kilometers (30,000 ft) and so the outlet air temperature actually decreases with altitude up to nine kilometers then increases.
Forced convection: In general convection of heat from a surface to the local ambient air decreases as density decreases. Below nine kilometers the temperature decreases more than the density so surfaces are generally cooler than at sea level. Above nine kilometers the temperature levels off and the density continues to drop.
Forced convection, the transfer of heat from a surface to a moving fluid, is a function of the fluid properties (,µ,k,cp), the velocity of the fluid, v and the surface geometry. A typical empirical correlation for forced convection takes the form.
where the exponents n and m are less than one and the factor C ranges from .036 to 1.86. For a fixed geometry air cooled system operating in the atmosphere the only quantities that effect convection that vary with altitude are the density and the velocity. Both these quantities are accounted for in the Reynolds number,
Since the viscosity µ and the thermal conductivity, k vary only slightly with altitude the heat transfer coefficient, h varies only with the mass flow rate, .
For turbulent forced convection inside a passage the Nusselt number, NNu is given by
So the heat transfer coefficient, h varies with the mass flow rate to the 0.8, h~ 0.8 which is valid for flow over flat plates as well as inside passages. In the example shown in Figure 8, the conventional fan/system shown in Figure 6 is used to cool a 500 Watt load during a Hot day to obtain a 10°C air to surface gradient at sea level. The effect of the decrease in advection is included in Figure 8.
Figure 8: Forced convection an example
Summary
Air cooling at high altitude requires a more detailed analysis of the air, fan and system characteristics than sea level cooling. Although the air density decreases dramatically above nine kilometers the air temperature typically decreases sufficiently up to nine kilometers to compensate for the decrease in density. Fan pressure decreases with density. Conventional fans operate at almost constant volume flow rate as density changes. “Slip” fans operate at higher volume flow rates as density decreases. Fan selection for cooling at altitude is similar to sea level fan selection except that the mass flow rate is greatly reduced. The use of a “slip” fan can greatly reduce the fan power requirements over the operating altitude range. The air temperature rise (advection) and the heat exchanger performance (convection) are both adversely affected by decreasing density. By accounting for the variation in air properties, fan performance, system pressure drop, advection and convection the feasibility of air cooling at altitude can be readily determined from commonly available data.
References:
| 1. | Incropera, F. P. and Dewitt, D. P.,1981 Fundamentals of Heat and Mass Transfer, John Willey & Sons, New York |
| 2. | Gerhart, P. M. And Gross, R. J.,1985, Fundamentals of Fluid Mechanics, Addison-Wesley Publishing Company, Massachusetts |
| 3. | Rotron Custom Airmovers Catalog, 1992, New York |
| 4. | Chapman, A. J., 1974, Heat Transfer, Macmillan Publishing Company, New York |
| 5. | Military Standard 210C, Climatic Information To Determine Design And Test Requirements For Military Systems And Equipment, 1987, Electronic Systems Center, Hanscom AFB, MA |