Heat transfer in electronic packages is a complex problem involving a network of resistive paths for the various laminated structures, bonding adhesives, lead frames, and attachment mechanisms, such as ball grid arrays. However, despite the multitude of materials and interfaces within an electronic package, the largest thermal resistance, and consequently the controlling resistance in the path between the source and the sink, is generally the boundary layer or film resistance at the solid/fluid interface. Given the inverse relationship between the film resistance and the product of the heat transfer coefficient and the surface area, an increase in either the heat transfer coefficient or the surface area results in increased heat transfer and lower operating temperatures. In natural convection applications the best method for reducing film resistance is achieved by increasing the effective surface area for convective heat transfer through the use of heat sinks and extended surfaces.
Heat sinks offer a low cost, convenient method for lowering the film resistance and, in turn, maintaining junction operating temperatures at a safe level for long term, reliable operation. Unfortunately, the selection of the most appropriate heat sink for a particular application can be very difficult, given the many design options available. Thermal analysis models, ranging from simple empirically-derived correlations to powerful numerical simulation codes, can be used to analyze the thermal performance of heat sinks for a given set of design conditions, however, analytical models, based on the fundamental formulations for conservation of mass, momentum and energy, provide distinct advantages over most other models. The advantages of analytical modeling include speed, accuracy, ease of use and simplicity of coding, especially for web based software tools.
Analytical models are presented for calculating natural convection heat transfer as a function of the geometry, material properties, and the boundary and ambient conditions for the three heat sink geometries shown in Fig. 1, the circular- and square-finned radial heat sink and the plate fin heat sink. Options are available to calculate both the total heat flow rate, Q, and the isothermal baseplate temperature, Ts. through the independent control of the geometric parameters. Options for the solutions include non-isothermal fin temperatures to account for fin effects, as well as radiation heat transfer (radial fin) and an insulated back surface on the baseplate (plate fin).
 |
Figure 1. Plate fin and radial fin heat sinks.
Background
Plate fin heat sinks considered in this analysis consist of evenly spaced, vertical fins in perfect thermal contact with a baseplate of uniform thickness where an isothermal boundary condition is uniformly applied over the back surface of the baseplate. Radial fin heat sinks are assumed to consist of evenly spaced cylindrical or square fins in perfect thermal contact with a concentric, isothermal circular support cylinder.
The Biot number, given as Bi = h � t/k, can be used to assess the validity of the isothermal assumption in the baseplate or the support cylinder of the heat sink. A Bi < 0.1 is generally used as a measure of one-dimensional heat flow and, in turn, an absence of temperature gradients within the baseplate. Typical heat sink properties lead to Biot numbers less than 0.1, thereby validating the assumption of an isothermal baseplate.
The total heat flow rate from the heat sink, Q, is related to the isothermal baseplate or support cylinder temperature by:
|
| Nomenclature | |
| A | surface area, (m2) |
| Bi | Biot number, = ht/k |
| b | spacing between adjacent fins, (m) |
| d | diameter of support cylinder, (m) |
| D | fin outer diameter, (m) |
| g | gravitational acceleration, (m/s2) |
| h | convective heat transfer coefficient, (W/m2 K) |
| H | height of heat sink, (m) |
| k | thermal conductivity, (W/mK) |
| L | length of heat sink, (m) |
| Nf | total number of fins |
| Nub | Nusselt number, = hb/k |
| n | combination parameter |
| Q | heat flow rate, (W) |
| Ra*b | modified Rayleigh or Elenbaas number, = g� |
| S* | dimensionless conduction shape factor |
| Ta | temperature of ambient air, (K) |
| Ts | surface temperature of heat sink, (K) |
| temperature difference, Ts – Ta, (K) | |
| t | fin thickness, (m) |
| tbp | baseplate thickness, (m) |
| W | width of heat sink , = tNf + b (Nf – 1), (m) |
| Greek Symbols | |
| thermal diffusivity, (m2/s) | |
| � | thermal expansion coefficient, (1/K) |
| v | kinematic viscosity, (m2/s) |
| Subscripts | |
| bl | boundary layer |
| fd | fully developed |
| IN | inner surface |
| OUT | outer surface |
| HS | heat sink |
The average convective heat transfer coefficient over the wetted surface of the heat sink, h, must be calculated as a function of the geometry and boundary conditions.
The thermal performance of the heat sink is calculated based on a dimensionless heat transfer rate, related to the heat transfer coefficient by:
|
where the spacing between adjacent fins, b, is the characteristic length. The Nusselt number is calculated as a function of the Elenbaas Rayleigh number, a dimensionless buoyancy-driven flow parameter defined as:
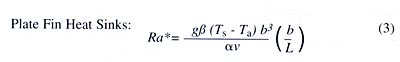 |
 |
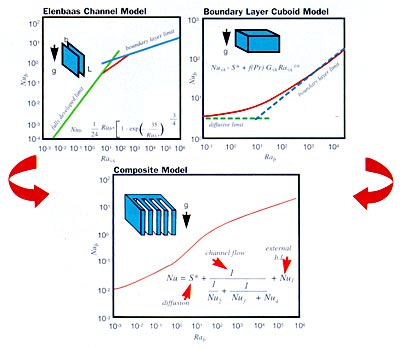
The total heat flow rate from the heat sink is calculated based on contributions from diffusion, channel flow and external boundary layer flow using the general expression:
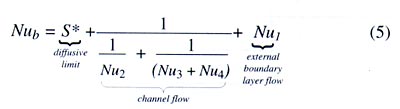 |
where S* is the dimensionless shape factor, Nu2 , is the boundary layer contribution for internal, vertical surfaces, Nu3 , is the heat transfer associated with fully developed flow, Nu4 is the heat transfer from the channel control surfaces, and Nu1 is the heat transfer from all external, unbounded surfaces.
Final results are presented in dimensional terms for either the total heat flow rate, Q, or the isothermal baseplate temperature, Ts, as well as in dimensionless terms for Nub vs . Ra*.
Models
Plate Fin Heat Sinks
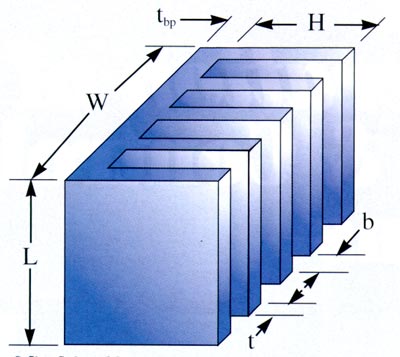
A simple plate fin heat sink, as shown in Fig. 2, has six independent geometric parameters that can be varied in any design; fin thickness, height, length, and spacing as well as the thickness and width of the baseplate. In addition to the design challenges associated with determining the most appropriate heat sink geometry, the flow dynamics resulting from buoyancy induced flow can vary significantly depending on the various surface regions of the heat sink and the operating range of the Rayleigh number.
2. Plate fin heat sink.The works of Elenbaas [1, 2] first examined methods of combining a natural convection boundary layer solution with a fully developed solution for vertical plates (Elenbaas, [1]) and channels of various cross sections (Elenbaas, [2]). The method proposed by Elenbaas for natural convection between parallel flat plates, combines the fully developed Nusselt number (Nu C1 Ra) with a flat plate boundary layer solution (Nu
C2 Ra 1/4) in a form that allows one to easily move between these two limits:
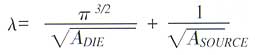 |
Churchill [3] achieved a similar result by using a blending procedure based on Churchill and Usagi [4], where the fully developed and boundary layer solutions for the Nusselt number are combined as:
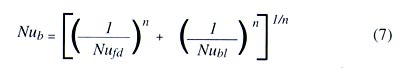 |
where n is a combination parameter, typically in the range of 1.5 – 2.0, such as n = 1.5 (Churchill, 1977), n = 2 (Bar-Cohen and Rohsenow, [5]), n = 1.9 (Raithby and Hollands, [6]).
Although these models provide a mechanism for determining the rate of heat transfer for specific geometric conditions such as cuboids in free space or natural convection between isothermal parallel plates, by themselves these models do not provide a solution to a general system consisting of internal and external isothermal surfaces cooled by natural convection. Karagiozis [7] presented a procedure for calculating heat transfer from rectangular and triangular finned surfaces where he recognized the importance of combining limiting solutions over three distinct ranges of Rayleigh number. The resulting composite equation for Nusselt number was based on heat sink geometry, fluid properties and four fitting parameters to smoothly integrate the limiting solutions and to plate overcome inherent “abnormalities” in the solution procedure. The fin heat sink model developed by the authors and as shown in Fig. 3, combines the parallel plate model of Elenbaas [1, 2] with the external natural convection models of Yovanovich [8, 9] to provide a simple, accurate model that predicts heat sink performance over a wide range of Rayleigh number using no adjustable fitting parameters.
Figure 3: Modeling procedure.Natural Convection from Radial Fin Heat Sinks
A radial fin heat sink, as shown in Fig. 4, consists of a common circular cylinder that transfers heat to a series of evenly spaced circular cylinders. Advantages of this style of heat sink include, an ability to maximize surface area within a relatively small overall volume, a minimization of constriction resistance from the source to the fin surfaces given the circular nature of the heat sink, and a reduction of the dependency on heat sink alignment given the omni-directional geometry of the heat sink.
Figure 4: Radial fin heat sink.The convective boundary formed between a radial fin heat sink and the fluid consists of four different types of component surfaces, i.e. lateral fin surfaces, support cylinder surfaces, fin rim surfaces and end surfaces. The combination of all lateral fin surfaces and support cylinder surfaces are referred to as inner surfaces, while the fin rim surfaces and the end surfaces are considered as outer surfaces.
Despite the obvious differences in the geometry between the radial fin heat sink and the rectangular fin heat sink, the modeling procedures for determining the overall rate of heat transfer are remarkably similar. The most apparent difference between the two solution procedures is the influence of the central support cylinder on the heat transfer within the channels formed by adjacent cylindrical fin sections. These effects are relatively small and are accounted for in the modeling procedure by introducing a factor that compensates for the penalty in thermal performance in the region downstream of the support cylinder.
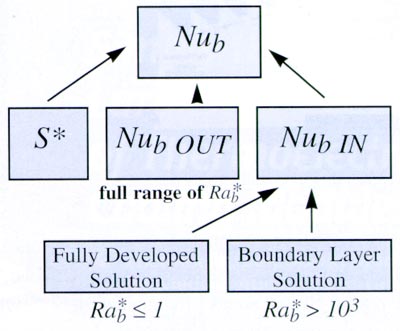
Using the same general principles described in the plate fin heat sink model and described in more detail in Wang [10] and Wang et al. [11], the overall Nusselt number for a radial fin heat sink can be obtained by combining the three component solutions, as shown in Fig. 5: the heat transfer from the inner surface, the thin boundary layer heat transfer from the outer surface and the diffusive limit.
Figure 5: Radial fin heat sink flow chart.
Web Tools
While the models described in the previous sections are relatively easy to implement in a spreadsheet or compiled program environment, the speed of computation and the minimal memory requirements associated with the analytical models makes them ideally suited for real time, web-based simulation tools. The heat sink models are programmed using a combination of Javascript for I/O requirements and CGI scripts for the simulation engine.
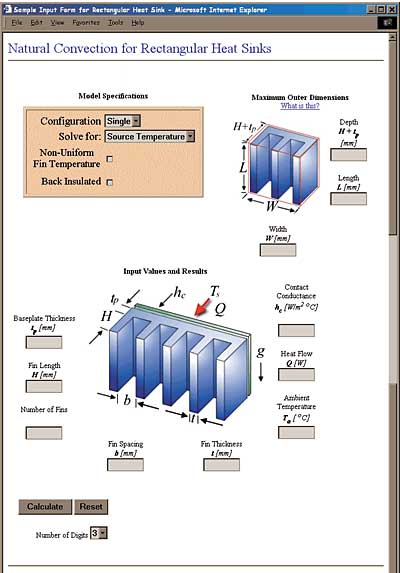
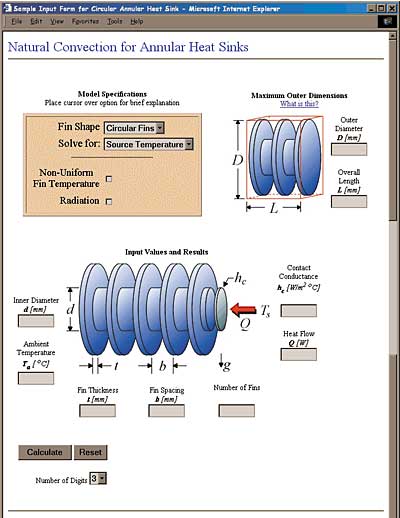
The interactive, real time solution tools described here, plus an extended set of complementary tools are available at the Microelectronics Heat Transfer Laboratory web site, http://www.mhtl.uwaterlooo.ca. and/or the website of Ideal Answers, http://www.idealanswers.com/. Figures 6 and 7 show examples of the graphical user interface for the plate fin and radial fin heat sink calculators, respectively.
Figure 6: Web-based plate fin heat sink calculation tool.
Figure 7: Web-based radial fin heat sink calculation tool.The models are easy to use and provide a convenient procedure for determining fin temperatures and heat flow rates for a wide range of geometries and boundary conditions. In addition to the basic I/O screens shown in Figs. 6 and 7, a details page is provided that lists problem specific information including temperature corrected fluid properties, a summary of the system geometry, performance data in both dimensional and dimensionless form, fin efficiency, and the overall thermal resistance of the heat sink.
Summary
Analytical models are presented for determining the thermal performance of plate fin and radial fin heat sinks cooled by buoyancy driven flows. Web-based, real time simulation tools are available that allow access to a wide range of simulation tools, including models for predicting thermal performance specifications of plate fin and radial fin heat sinks. These models provide a convenient and accurate procedure for sizing heat sinks and performing parametric assessments of design changes on thermal performance.
References
1. W. Elenbaas, 1942, “Heat Dissipation of Parallel Plates by Free Convection,” Physica, Vol. IX, No. 1, pp. 1 – 28.
2. W. Elenbaas, 1942, “The Dissipation of Heat by Free Convection – The Inner Surface of Vertical Tubes of Different Shapes of Cross-Section,” Physica, Vol. IX, 1942, pp. 865 – 874.
3. S.W. Churchill, 1977, “A Comprehensive Correlating Equation for Buoyancy-Induced Flow in Channels,” Letters in Heat and Mass Transfer, Vol. 4, pp. 193 – 199.
4. S.W. Churchill and R. Usagi, 1972, “A General Expression for the Correlation of Rates of Transfer and Other Phenomena,” AIChE Journal, Vol. 18, pp. 1121 – 1128
5. A. Bar-Cohen, and W. M. Rohsenow, 1984, “Thermally Optimum Spacing of Vertical, Natural Convection Cooled, Parallel Plates,” ASME Journal of Heat Transfer, Vol. 106, pp. 116-123.
6. G.D. Raithby and K.G.T Hollands, 1975, “A General Method of Obtaining Approximate Solutions to Laminar and Turbulent Free Convection Problems,” Advances in Heat Transfer, Vol. 11, Academic Press, New York, pp. 264 – 315.
7. A.N. Karagiozis, 1991, “An Investigation of Laminar Free Convection Heat Transfer From Isothermal Finned Surfaces,” Ph.D. Thesis, Department of Mechanical Engineering, University of Waterloo, Waterloo, Canada.
8. M.M. Yovanovich, 1999, “Natural Convection From Isothermal Convex Bodies: Simple Models for Bounds on Body-Gravity Function,” AIAA National Heat Transfer Conference, Aug. 15-17, Albuquerque, NM.
9. M.M. Yovanovich and K. Jafarpur, 1993, “Bounds on Laminar Convection from Isothermal Disks and Finite Plates of Arbitrary Shape for all Orientations and Prandtl Numbers,” Fundamentals of Natural Convection, ASME HTD Vol. 264, pp. 93-110.
10. C.-S. Wang, 1997, “Laminar Natural Convection Heat Transfer from Isothermal Horizontal Cylinders with Annular Fins,” Ph.D. Thesis, Department of Mechanical Engineering, University of Waterloo, Waterloo, Canada.
11. C.-S. Wang, M.M. Yovanovich and J.R. Culham, 1999, “General Model for Natural Convection: Application to Annular-Fin Heat Sinks,” ASME Journal of Electronic Packaging, Vol. 121, No. 1, pp. 44 – 49.