Clemens J.M. Lasance
Philips Research Laboratories Emeritus
The last time the subject of my column was: ‘Most of us don’t live in wind tunnels, neither in the world of Nusselt.’ I promised more comments about the (mis)use of the heat transfer coefficient h in real-life applications where we are dealing with multiple sources, anisotropic PCBs and multilayers. In this column I would like to share with you my thoughts on something that bothered me from the moment I started research in the field of thermal management. It concerns the fact, as most of you know, that Nu is constant for fully-developed channel flow with constant boundary conditions, for example constant temperature or constant heat flux. This is a typical example of a purely academic problem because in practice we (almost) always have a mixture of the two due to lateral heat spreading in the channel wall.
Because Nu equals h∙D/k, with D the hydraulic diameter of the channel and k the thermal conductivity of the fluid, the consequence is that h is constant, hence, among other things, h is independent of the velocity. This strikes me as pretty strange. In my view, given the mere fact that we have defined h as a metric for heat transfer (per unit area per degree C), I would have expected that when the heat transfer increases so does the metric that describes it. If this is not the case, the obvious conclusion is that the way h is calculated is not correct, from a philosophical point of view at least.
Of course the heat transfer calculated using the constant h does change when the velocity changes, dependent on the boundary condition. For constant flux the fluid temperature decreases with increasing velocity, and hence the wall temperature decreases which means that the heat transfer increases. For constant temperature the fluid temperature equals the wall temperature far enough from the inlet, hence there is no heat transfer at all. Of course, because q = h∙A∙∆T, with A the heat transfer area, q is zero because ∆T is zero, even when h is constant. Nevertheless, my intuition tells me that the heat transfer coefficient should go to zero because there is no heat transfer.
Note: I had some interesting discussions with Bob Moffat, the ‘inventor’ of the adiabatic heat transfer concept [1]. I could not convince him of the way I looked at the problem. Hence, to prevent being seen as a Don Quixote: I don’t challenge the Nu being constant using the standard definition, I challenge the definition itself. I don’t even challenge its usefulness. My argument is not that hadiab is practical in this case, it is not. Of course nobody is going to use hadiab for channel flow; what I want to demonstrate is that the concept of constant h is incorrect, even if it is useful in practice! For many people the concept of God is useful but this does not automatically imply that God exists. As a bonus: Bob Moffat told me that in a time long past Bill Kays, his mentor, was of the opinion that h should go to zero when ∆T goes to zero. I am in good company!
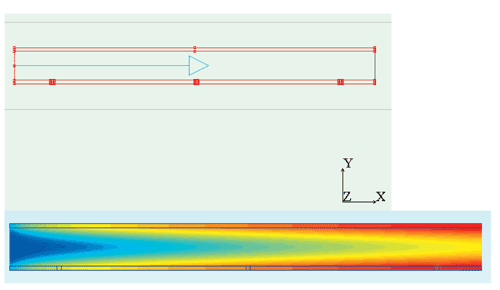
I asked myself the question: suppose we could define a physically correct adiabatic h, how would this h behave when we change the velocity? To address this I used a full-blown numerical analysis of fully-developed laminar flow inside two parallel plates. The idea is that we may consider the channel wall as consisting of many sources separated by an insulation layer of negligible thickness. Figure 1 shows the layout of the setup.
To ensure fully-developed flow a number of requirements should be met, and I had many interesting discussions with Bob Moffat on how to realize this because even a small departure from fully-developed would probably render the results useless. For the experts: based on the eigenfunction solutions, x+ should be at least 0.2 to guarantee fully-developed flow. Following his advice I used the following input data:
Channel width: 8mm
Channel length: up to 250 mm
Fluid velocity: 2-20 cm/s
Adiabatic cell size: 0.25-1 mm
Uniform heat flux: 100 W/m2
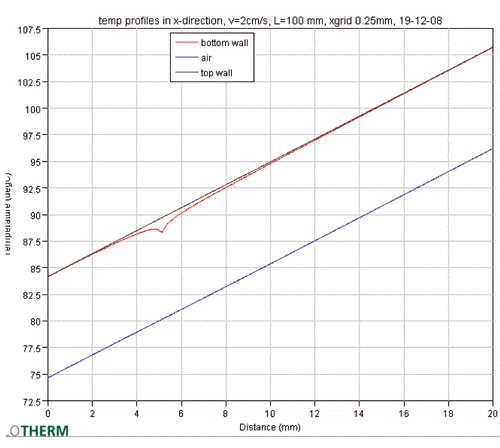
The problem to be addressed is: How can we define a local adiabatic h? By adhering to its definition: the reference temperature is found by switching off the dissipation and recording the adiabatic or unpowered temperature: q = hadiab∙A∙(Twall-Tadiab). In our setup this is realized by setting the lateral thermal conductivity of the channel wall to ‘zero’ and perpendicular to this to ‘infinite’, to prevent lateral heat spreading altogether. Additionally, starting from a uniform heat flux for the channel walls, an extra negative source was added to the adiabatic cell to result in zero heat flux in order to find the local adiabatic temperature. Of course one of the parameters is the size and location of the cell. The smaller the cell, the less the effect of setting the dissipation to zero has on the downstream flow. Figure 2 shows a plot of the channel wall temperatures when one adiabatic cell on the bottom wall at position 5 mm. Also the air temperature at midplane is shown.
As a check, the mean mixed temperature for several positions in the channel and the resulting standard Nu number were calculated. It turned out that the Nu value was within 1% of the theoretical value (8.235), giving confidence to the calculations.
The h based upon this Nu can then be calculated to be 13.4 W/m2K.
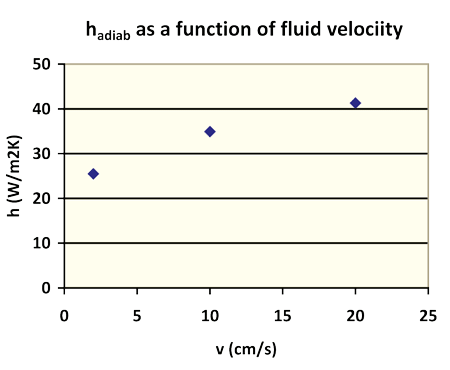
The question is: how does hadiab behave when we change the velocity? Well, just as I thought: it depends on it. Figure 3 shows some results.
From the graph you see that for zero velocity there is still appreciable heat transfer, caused, of course, by pure conduction through the fluid. However, this conduction contribution is not easy to calculate because it is not 1D! The 1D conduction heat transfer would result in an effective h of roughly 3 W/m2K; because of heat spreading from the adiabatic cell, this value is much larger in practice.
But this is not the end of the story. Some interesting questions pop up, such as:
- What happens when the cell width goes to zero?
- What is the influence of lateral conduction in the fluid?
- What exactly happens when we apply a step function in the heat flux along the wall with the adiabatic heat transfer coefficient along the wall?
- How does the cell width influence the results?
- Back to the original question. I personally did not buy an h that is constant whatever the velocity, it just does not make sense. But I wonder also if this is just a matter of semantics, in other words, should a heat transfer coefficient indeed describe heat transfer?
I would appreciate your opinion.
REFERENCES
Moffat, R., and Azar, K., “Evaluation of Different Heat Transfer Coefficient Definitions,” ElectronicsCooling, Vol. 1, No. 1, June, 1995.