There must be an ideal world
A sort of mathematicians’ paradise
Where everything happens
As it does in textbooks
— Bertrand Russell
This is the third column devoted to the sense and nonsense of correlations. My earlier comments [1] regarding Russell’s quote are maybe worth repeating: “Generations of mechanical engineers have been educated to use the correlations that fill the textbooks Russell is mentioning because: ‘For convenience of engineering applications, correlation equations are developed over the entire range of dimensions and for any Pr-number.’ Unfortunately, for a thermal designer, real-life is more like hell than paradise, and hence it is high time to address the question, ‘How convenient are these correlations in real-life?’ When it comes to thermal management of electronic systems, the answer is that correlations are not only useless but also dangerous because their use by non-experts gives a false sense of safety.” Maybe “useless” is a bit exaggerated. As one reviewer put it: “Correlations can be used to provide a basic sense of how a system might react under some simple geometries and equivalent inputs and can potentially yield important information of general behavior.” The problem is that in practice simple geometries are not the rule, but the exception.
The paper goes on: “Suppose some alien wants to study the heat transfer behaviour of a flat heat sink cooled by air. He, she or it never had the opportunity to read standard textbooks on heat transfer. The alien varies the parameters of interest, for example the power q and the length L, measures the temperature rise, and comes up with the following equation:
providing exactly the information needed: the dependency of the temperature rise on the power and the heat sink dimensions.” The alien would be very surprised if someone told him to present the results in the following way, because it should be “more convenient for engineering applications”:
The author fully agrees with the comments made by Botterill [2] some 20 years ago: “Give preference for the most simple form of representation instead of the much more ambitious generalisations.” The same way of working Bill Kays and Bob Moffat at Stanford proposed already 40 years ago (personal communication): “Simpler is better, hence don’t plot Nu vs. Re but h vs. v.”
I would like to mention two other flaws of publishing correlations: loss of original data and danger of imposing a slope. The first flaw is easily understood. Read any article in ASME journals and try to get hold of the original test data. You can’t. Additionally, because all data points are first made dimensionless and then put on double-log paper, details are lost. Following Bob Moffat: “Years of poorly controlled and inadequately described experiments have filled the literature with data that appear to be ‘comparable’ but are not, with the consequence that the average designer seems to accept the fact that there will be always ± 20-50% scatter in heat transfer data.” In general, you can be confident that the original data did not show this large scatter.
The second flaw is less obvious. In mathematics, everyone strives towards separation of variables because doing so simplifies the solution. Not so in heat transfer. This becomes immediately obvious when looking at the following general Nu-Ra equation describing general heat transfer for natural convection, Nu = C.RaN:
where ΔT, L and k are common to both sides of the equation. This confounding of parameters has led to a curious observation, originally formulated by Rowe [3] and discussed by Wilkie in two papers [4,5]. The results presented by Rowe are very illustrative. He used data points from random number tables for the parameters that are common to both sides of a set of dimensionless equations, and plotted the ‘results’ on log-log paper. After ignoring a few rogue points, combinations such as Nu-Re, Nu-Gr and several others clearly showed a correlation where obviously there can be none. Wilkie reinterpreted Rowe’s data as follows. If Equation (3) is plotted on log-log paper, a straight line is obtained. He showed that by varying L a slope of 1/3 is imposed. It is interesting to note that this slope is close to the often-quoted values in the literature for turbulent heat transfer. In his second paper, Wilkie extended the analysis to the situation where the three common variables L, ΔT and k are varied simultaneously, which could be the case in natural convection studies, and presented some convincing arguments that some often-used correlations (especially for turbulent natural convection heat transfer) should be regarded with caution. If the observed slope from an experiment is not significantly different from the imposed slope (as determined by proper statistical means), no conclusion can be drawn about the correlation between the variables that are common to both sides. As a consequence, randomly chosen values of the heat transfer coefficient could produce an apparent correlation with an index given by the imposed slope, or, alternatively, a slope of magnitude different from the imposed slope could remain undetected. Especially when a large data set is being used, for example when one of the common variables has been varied over a wide range, the danger of an imposed slope becomes relevant. This is clearly the case for the famous correlation for natural convection from horizontal cylinders spanning more than 13 decades in Gr presented by McAdams [6] almost 60 years ago. Note that the upper-half slope is 1/3, exactly the exponent for turbulent heat transfer, but also of the imposed slope.

One of Wilkie’s recommendations is to vary only those parameters that are not common to both sides. One of my recommendations is to refrain from common-variable formulae altogether.
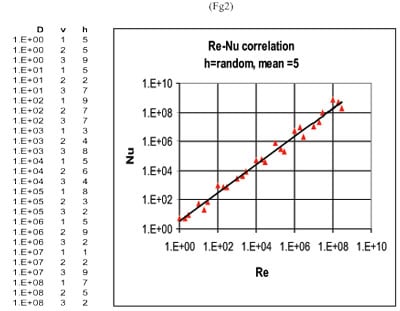
The following simple example illustrates the problem raised by Rowe and Wilkie in a convincing way. Suppose we want to study turbulent pipe flow in a strange world where all physical properties happen to be 1. We set the dissipation to 1 W, vary the diameter over quite a big range, the velocity at three levels and measure the temperature rise. The ratio q/ΔT provides us with the heat transfer coefficient h. For reasons yet unknown in this strange world to be explored, whatever we choose for D and v, h varies between 1 and 10 in a random way. Let us now plot Nu=h·D/k against Re=v·D/v, with k and v set to 1.
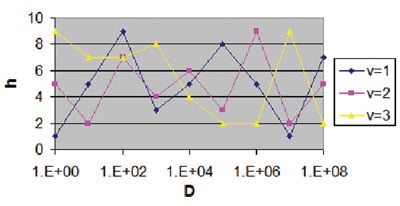
I hope the reader understands that the essential point here is not the value for Nu and Re (can be scaled of course to suit any realistic world) but the fact that D varies over a large range (but not as large as in the McAdams example cited above). From the graph a clear correlation between Nu and Re becomes apparent, namely Nu=C.ReN, with C=1.67 and n=0.97. In other words, the graph suggests that h is about proportional to v, which is clearly not the case. Figure 3 shows a ‘traditional’ plot of h against D with v as parameter from which it is immediately obvious that there is no correlation at all.
Conclusions
It should be noted that correlations have proven their value over the last century in a wide range of applications, some of which are not only of academic interest. However, when focusing on electronics cooling, we face a different situation. There is one major reason why correlations are not recommended: the inherently complex geometries. Correlations make sense only when three conditions are fulfilled [1]: similarity, congruency and the boundary layer approximation. In most practical cases these conditions are not met, and if so, the number of required dimensionless groups becomes intractable. The bottom line is: geometrically and physically complex phenomena cannot be described by simple equations.
This column focuses on a peculiarity of correlations: a non-physical slope can be imposed when attempting to develop relations using common-variable formulae leading to wrong conclusions. A simple example
convincingly demonstrates this phenomenon.
References
[1] Lasance C., “Sense and Nonsense of Heat Transfer Correlations Applied to Electronics Cooling,” Proc. 5th Eurosime, Berlin, 2005.
[2] Botterill J., “No Substitute for Experimentation – Despite the Fallibility of Experimenters,” Exp. and Thermal Fluid Science, Vol. 3, pp. 463-466, 1990.
[3] Rowe P., “The Correlation of Engineering Data,” The Chem. Eng., No. 166, March, pp. CE 69-CE76, 1963.
[4] Wilkie D., “The Correlation of Engineering Data Reconsidered,” Int. J. Heat & Fluid Flow, Vol. 6, pp. 99-103, 1985.
[5] Wilkie D., “Some Doubtful Natural Convection Correlations,” Proc. 9th Int. Heat Transfer Conf., Jerusalem, pp. 555-560, 1990.
[6] McAdams W., Heat Transmission, 3d Edition, McGraw-Hill, p. 176, 1954. l






