Thermal fact: the temperature dependence of the specific heat can be very large.
Thermal fairy tale: neglecting this dependence can be a serious problem.
In my Tech Data column of May 2003 the thermal capacitance was discussed. I will repeat here the most relevant issues before discussing its temperature dependence.
The thermal capacity (or heat capacity) Cth is defined as:
Cth = V ρcp [J/K]
where:
V =volume (m3)
ρ= density (kg/m3)
cp = specific heat (J/kgK) at constant pressure (the usual situation)
The essential point to keep in mind is that only the product ρcp is important. Handbooks often quote only the individual values for ρ and cp, and you will notice that large differences exist between materials. For example, let’s compare platinum and magnesium. Their densities are respectively 21,400 and 1740 kg/m3, their specific heats 1050 and 130 J/kg K, big differences, , but their thermal capacities are 2.9 106 and 1.7 106 J/m3K, much less than a factor of two apart. What is the reason you may wonder? Essentially, the specific heat is linked to the internal energy (such as rotational and vibrational energy) of a molecule. More correctly, the specific heat is the change in the internal energy per unit of temperature change. The more degrees of freedom the molecule has, the more energy it can store. Now suppose we have a material with a high density, which means that the molecules are very close to each other. Certainly this reduces the ability to vibrate. In other words, the material has a low specific heat. The result is that the product ρcp falls within a relatively narrow margin. Gases are a different story. ‘Free’ is ‘free’, and beyond a certain freedom it is only the density that counts. Table 1 provides some rules-of-thumb for certain classes of material.
|
Table 1. Orders of magnitude for ρcp
Hence, for first-order guesses, the ρcp of all solids of interest lies between 1.5 and 3.5 MJ/m3K, and don’t bother about the enormous differences in either ρ or cp. [1]
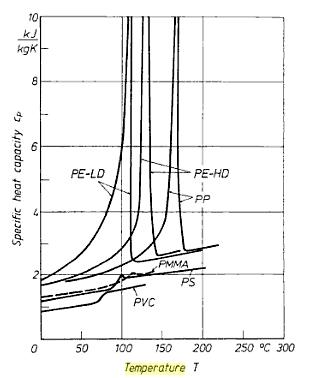
Now onto the temperature dependence of the heat capacity Cth. For time-dependent analyses, often a large temperature gradient has to be covered, and hence the question is relevant if we should take into account the temperature dependence of the heat capacity. In some cases of practical interest we should also consider a phase change, for example for temporarily heat storage (e.g. solar load control) or for heat sinks filled with phase change material. Everyone who has ever looked up a graph of cp versus T for some materials including their melting point or melting range, will have been surprised after noticing its weird shape. Figure 1 shows some examples.
Figure 1. The temperature dependence of the specific heat for some plastics.
(PE: Polyethylene, PP: Polypropylene, PMMA: Polymethylmetacrylate, PS: Polystyrene, PVC: Polyvinylchloride)
In the old days, using SPICE-like codes for thermal analysis, one was tempted to use a table of cp versus T to describe the dependence. However, often one ran into serious numerical problems because of the sharp transition points, until one realizes that in practice we are dealing with the integral of cp, in other words, it is the area below the curve that matters. One can easily imagine that this integral is a much more smooth function of T, the distinct peak hardly contributes to the integral. Again in the old days, using a table of the integral ∫ρcp instead of a table of cp aloneversus temperature solved the numerical problems. To be honest, I don’t know how this problem is handled in today’s codes.
From a thermodynamic point of view it is really the change in enthalpy that governs the temperature behavior of a substance heated or cooled in time. For a phase change material the equation is:
ΔH=m ∫cpdT+mΔh
with h the specific latent heat of fusion. It should be noted that in practice often the second term is much bigger than the first term, proving the benefits of using melting as an efficient form of heat storage.
In summary, the often strong temperature dependence of the specific heat is nothing to worry about.
[1] Another consequence of the limited range of the productis shown in the Tech Data column of August 2007, where a graph is shown of the thermal diffusivity (k/ρcp) versus thermal conductivity (k), resulting in almost straight lines.