By: Clemens J.M. Lasance; Guest Editor
The answer to the question stated in the title is both! It all depends on whether or not your situation is truly similar to the situation described in the book (physically congruent, fluid mechanically and thermally similar). Very few heat transfer books provide detailed dimensions and flow conditions for the experimentally observed data they contain – more often they simply describe the overall situation briefly and idealistically.
In other words: it all depends if you believe in the axioms or postulates that are, more often than not, hidden in the introductory chapters. I found it enlightening to see the parallelism with some other Holy Books, and hence this column is about why people believe in books or trust gurus (I do not belong to this category of course). It is all about the acceptance of axioms or assumptions. In mathematics, an axiom is any mathematical statement that serves as a starting point from which other statements are logically derived. In common language, an axiom is a premise so evident as to be accepted as true without controversy.
However, progress in science has learned otherwise. It is not correct to say that axioms are propositions that are regarded as true without proof. Rather, it is better to look at axioms as a set of constraints. If any given system (or book) satisfies these constraints, then one is in a position to instantly know a great deal of extra information about this system (or book). Applied to heat transfer this means that if and only if the physical situation conforms to the assumptions does the experimenter have the right to assume that the predicted results will be obtained. That means much more than simply matching Nusselt (Nu) and Reynolds (Re) numbers. Specifically, all analytical (and numerical) studies assume uniform flow velocity with a specified turbulence (often zero), uniform temperature and the origins of the velocity boundary layer and the thermal boundary layer on the surface.
Let me quote from my column of April 2010 [1]: “Having read myriads of papers/articles/books/reports on thermal management I feel there is a lot of misunderstanding about what really should drive a sound approach of how to tackle the thermal problems that land on the desk of thermal designers.” The problem, in a nutshell, is that the handbooks are inherently based upon a set of constraints that are not satisfied in real-life. Even more important, this set is rarely described. When you believe in the following axioms, then the Holy Books of Heat Transfer are consistent and comprise a wealth of information, very useful for a basic understanding of the physics.
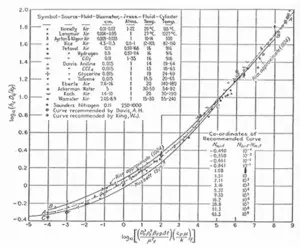
Figure 1 – Nu-Gr correlation for horizontal cylinders [6].
- Uniform boundary conditions, either constant temperature or flux
- Uniform approach flow with a degree of turbulence as close as possible to zero (that’s why research type wind tunnels are huge).
- (Very) simple geometries: smooth, flat and thin plates, parallel plate channels, pipes
- Single source, especially for natural convection
- Constant properties
- Fan dynamics based on airflow chamber testing
- Extended surfaces based on Murray-Gardner assumptions
- ‘Complex shapes’ means there exist an analytical solution
- Heat spreading limited to one-layer, one-sided heat transfer
- Radiation diffuse and grey
For many fields of heat transfer, such as turbulence, boiling, heat exchangers, channel flow, etc., these axioms form a sound base. Not so for thermal management of electronics. When your situation is consistent with all of the assumptions described above (geometric, fluid mechanic and thermal), then the presented results can be immediately useful. Otherwise, they must be taken only as “data taken along an idealized path” through the real world that you are working in. It is then up to you to decide how much to raise or lower the provided values of h.
There is another aspect of heat transfer theory that deserves attention, with their own axioms, and this is correlation theory that tends to pollute every heat transfer book or paper. A long time ago I coined the term ‘Correligion’ because that is exactly how it feels to someone like me who is not trained as a mechanical engineer but as a physicist: a religion, based on axioms that are subject to serious doubt in practice. Quoting Dr. Bob Moffat: “Years of poorly controlled and inadequately described experiments have filled the literature with data that appear to be ‘comparable’ but are not. It is the result of standard practice: all data ‘must’ be made dimensionless and collapsed on log-log paper……The average user seems to accept the fact that there will be always ± 20-50% scatter in heat transfer data…..Reynolds number scaling is much more subtle than many heat transfer researchers think.” Why this scatter, you may wonder, that would be unacceptable in other fields of science? Because it seems forgotten that correlations make only sense when they obey the following three axioms:
- Congruency
- Similarity
- The boundary layer approximation
- Ref [2] shows that in most practical cases especially the lack of congruency causes the problems. The axiom of congruency implies that all dimensions, velocities, times and forces should scale. Dr. Moffat and his students have published some interesting results, for example, that the accuracy of your correlation increases significantly when you scale also your wind tunnel. The consequence in practice? Suppose you want to study flow between two plates with a variable space. When you change this dimension, formally you should also scale the plate thickness, the plate area, and your wind tunnel!
In ref [3], I point to another phenomenon that puzzled me for a long time: the fact that Nu (and hence the heat transfer coefficient) is constant for fully-developed channel flow, independent of the velocity. As a physicist, this does not make sense to me. I showed that if you rewrite the local h in an adiabatic form, the results do make sense.
Another flaw, I would not call it an error, is the curious fact that by using dimensionless equations there is a danger of imposing a slope, caused by confounding of those parameters that are common to both sides of the equation by making the equation dimensionless, first discussed by Wilkie [5]. I discussed this flaw extensively in refs.[2] and [4], but I would like to repeat here an interesting interpretation of one of the famous and often cited graphs in one of the earliest Holy Heat Transfer Books [6], which is reproduced in fig. 1. Especially when a large data set is being used, for example when one of the common variables has been varied over a wide range, an imposed slope becomes clearly visible. In fig. 1, we see a correlation for natural convection from horizontal cylinders spanning more than 13 decades in Grashof (Gr) number. Note that the upper-half slope, which represents turbulence, is 1/3, which is exactly the exponent for the imposed slope. The conclusion that turbulent heat transfer scales with the same slope is not warranted at all. The point is that you get, by definition, the 1/3 slope if you randomly vary the heat transfer coefficient and put the results on double-log paper. Hence, is it a fact or a fairy tale that the turbulent heat transfer coefficient scales with the velocity to the power 1/3? You may not conclude this from the graph alone. What one should do, is to plot convective heat transfer coefficient (h) versus velocity (v), with the diameter as the parameter.
I quote here only one Holy Book. I could quote many others, but it suffices to say that I have read them all, including many that are specifically devoted to thermal management of electronics. None of them devote a chapter or even a paragraph to the problems designers are facing who have to deal with the complex geometries and the non-uniform boundary conditions, and the consequences thereof for applying the plethora of equations derived for simple geometries.
Disclaimer: I am not discussing the tremendous value of these books for other fields of heat transfer!
I challenge all readers to show me and the other readers that I am wrong. This, I hope, would start at last a discussion on a very important topic in electronics cooling: the huge gap what is required in real-life and what is found in holy books: “What did you learn in school today, dear little boy of mine?” “About little boxes made of ticky tacky, little boxes all the same.”
Note: the original version continued here with a discussion on how perfectly rational the arguments of believers in the real Holy Books are, provided the postulates are taken for granted. It continues with an overview of modern fiction-based religions such as the Tolkien Religion. This later discussion is not included here since it is considered to not fit within the framework of this magazine. The complete version may be obtained by contacting the author at lasance@onsnet.nu.
ACKNOWLEDGMENT
Many thanks to Dr. Bob Moffat who commented upon an early version. I gratefully used his valuable critic. Here is his recommendation when you still would like to use that impressive correlation, despite all the foregoing:
Be sure you know the following six things about the situation it describes:
- The Velocity Field (Reynolds number)
- The Fluid Properties (Prandtl number)
- The Shape of the Test Rig and the Specimens
- The Temperature Boundary Conditions
- The Temperature Initial Condition
- The Reference Temperature
REFERENCES
[1] Lasance C., Most of us live neither in wind tunnels nor in the world of
Nusselt ElectronicsCooling, April 2010.
[2] Lasance, C., “Sense and Nonsense of Heat Transfer Correlations Applied to
Electronics Cooling”, Proc. EUROSIME 2005, pp.8-16.
[3] Lasance C., Fully-developed channel flow: why is Nu constant?
ElectronicsCooling, September 2010.
[4] Lasance C., Does Your Correlation Have an Imposed Slope?
ElectronicsCooling, September 2011.
[5] Wilkie D., 1985, The Correlation of Engineering Data Reconsidered, Int. J.
Heat & Fluid Flow, vol.6, pp.99-103.
[6] McAdams W., 1954, Heat Transmission, 3d Edition, McGraw-Hill, p.176.