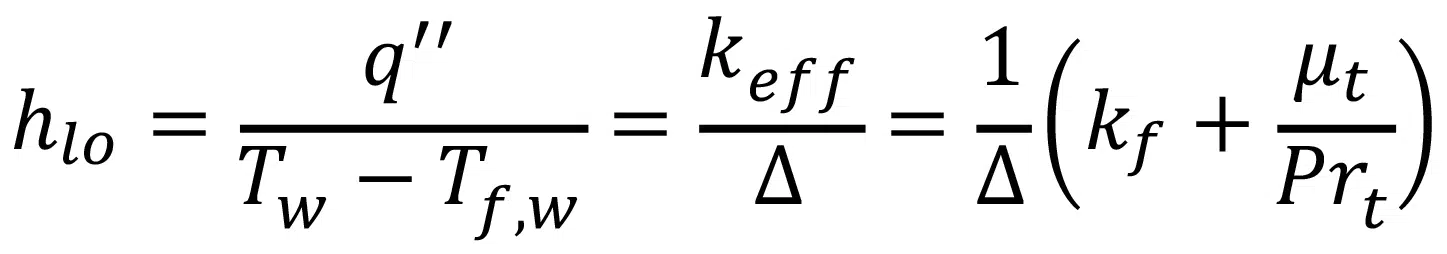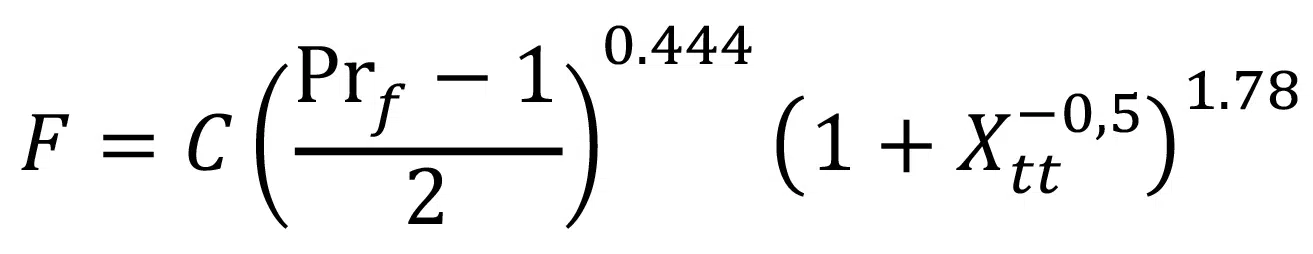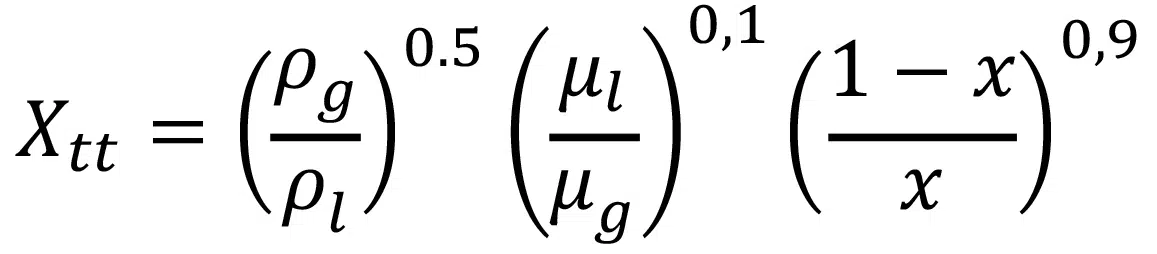Since the size of electronic components keeps on decreasing, the need for improved heat dissipation on these components keeps increasing. This dichotomy presents thermal engineers with a formidable challenge: how to design smaller coolers that dissipate more heat. Adding to the challenge, the fast-paced evolution of electronics means that the development time for the new cooler designs is shorter and shorter.
This article explores the combination of generative design and advanced two-phase cooling simulation techniques to efficiently create two-phase electronics cooling devices. The article starts with a discussion of the numerical models followed by a brief explanation of the generative design method. Finally, a proof-of-concept design is shown and discussed.
Two-phase cooling modeling
Over recent years, computational simulations have become an integral part of the design cycle for new products. The increase of computational power, in combination with the development of more advanced numerical models, enables the simulation of complex problems more accurately and faster than ever before. Adopting simulations during the design cycle greatly increases the efficiency of the development process from both cost and time points of view. When compared to experimental tests, simulations tend to be much more affordable and easily scalable, meaning that a much wider design space can be explored at a fraction of the cost.
When substituting experimental tests with simulations, the accuracy of the latter is key. By definition, simulations rely on models that only approximate physical behavior. As the complexity of models is often directly related to their performance and computational costs, choosing the correct models becomes a fundamental step in the design procedure. In conjugate heat transfer problems, the simulation of the solid and fluid components can be, to a certain degree, treated independently.
One common approach is to simulate the solid with a thermal resistance model, or more advanced numerical models such as finite elements, and approximate the fluid with a one-dimensional model along the flow channel, as depicted in Table 1. In this approach, the heat transfer between the solid and the fluid is calculated as the temperature difference along the channel multiplied by a convective heat transfer coefficient that is typically obtained from Nusselt correlations. The approach is computationally friendly because it avoids the direct computation of coolant behavior. However because the approach ignores local variations of fluid characteristics, such as boundary layers and turbulence, a design obtained using this approach is likely to be sub-optimal.
An alternative approach is to simulate both the solid and the fluid with a three-dimensional simulation code and solve for the full flow field in the channel. In this case, the two-phase flow is fully simulated on a detailed computational grid and the heat exchange between the solid and the fluid depends only on the temperature difference between the solid and the fluid cells adjacent to the wall. While computationally more expensive, the approach results in more detailed insight into the physics of the problem, thus allowing for more accurate results.
Compared to single-phase flows, two-phase flows present a much higher complexity. The interactions between the flow phases and the differences in physical characteristics of each phase make the simulation of a two-phase flow challenging. The simplest hydrodynamic model of a two-phase flow is the homogeneous model. This model postulates that the liquid and vapor phases are well mixed, move with the same velocity, and are thermodynamically in equilibrium. In essence, the two-phase flow is treated as a single-phase fluid. Alternatively, inhomogeneous multiphase models can be used. These models take into account the velocity slip between the vapor and liquid phases. This requires interface modeling and tracking, which result in a significantly higher computational cost. A comparison between both modeling approaches is given in Table 2, for a more exhaustive comparison see [4].
The general equations of multiphase flows consist of three transport equations, for mass, momentum, and energy, along with additional jump conditions at the interfaces between the vapor and liquid phases to close the system of equations. However, using the HEM, the two-phase flow is treated as a single-phase fluid with energy-dependent fluid properties along the channel. This reduces the system of equations to the single-phase Navier-Stokes equations in which the fluid properties are evaluated based on the local flow quality or local vapor fraction.
Regardless of which two-phase model is used, the heat transfer at the solid-fluid interface must be quantified. For this work, a new modeling approach was developed based on the two-phase multiplier concept of Lockhart and Martinelli [1], which imposes that:
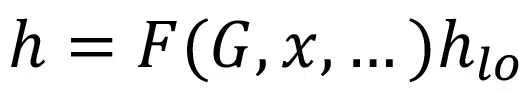
Where h is the actual heat transfer coefficient, hlo is the convection heat transfer coefficient when all mass is saturated liquid, which is evaluated through CFD simulation, and the function F(G,x,…) is a two-phase multiplier that acts as a correction factor to hlo.
Using a finite-volume, the local heat transfer coefficient between the wall and coolant is computed as
Where kf is the conductivity of the fluid, is the turbulent viscosity, Prt is the turbulent Prandtl number , typically equal to 0.85, and Tw,Tw,f are, respectively, the temperatures at the wall and the fluid next to the wall.
To model the two-phase multiplier, the correlation of Bennett and Chen is applied [5]:
Where Xtt is defined as
An additional scale factor C is introduced to temper the effect of local high quality values.
Generative Design
Generative design is an automated design process that requires minimal user input and interaction while generating high-performing designs. Generative design techniques explore the design space by iterating between different possible solutions and learning information at each iterative step to converge to an optimal design. From a set of inputs such as design space, objectives, and constraints, the algorithm explores different possible solutions for the problem, evaluates them, and uses the collected information to generate new and possibly better solutions. The cycle repeats until the best possible solution that respects the constraints is found. By evaluating each possible solution with advanced numerical simulations, the optimization algorithm becomes fully autonomous, thus reducing the human interaction in the design cycle to the set-up of the problem and the final design evaluation. To generate new possible solutions at each step of the design process, the information learned from analyzing previous solutions can be used in several different ways. Due to the limited user interaction with the design process, the human bias towards specific or well-known designs is avoided, thus allowing for a true complete exploration of the design space towards a potentially global optimum.
A popular generative design strategy is to apply topological optimization in which a design is generated by optimizing the material distribution in the design space. In broader terms, a part of the coolant space is transformed into a new material, which will define a new design. A major advantage of topological optimization is that it does not depend on an initial design; therefore, the design space can be freely explored and allow for a potentially better final design. In this work, the HEM two-phase model is used in combination with proprietary topology optimization software [2] to generate a high-performing two-phase cooling device. A gradient-based optimization algorithm is applied and manufacturing constraints, such as minimal feature size and other 3D printing restrictions, are enforced via manipulation of the design sensitivities.
Case study
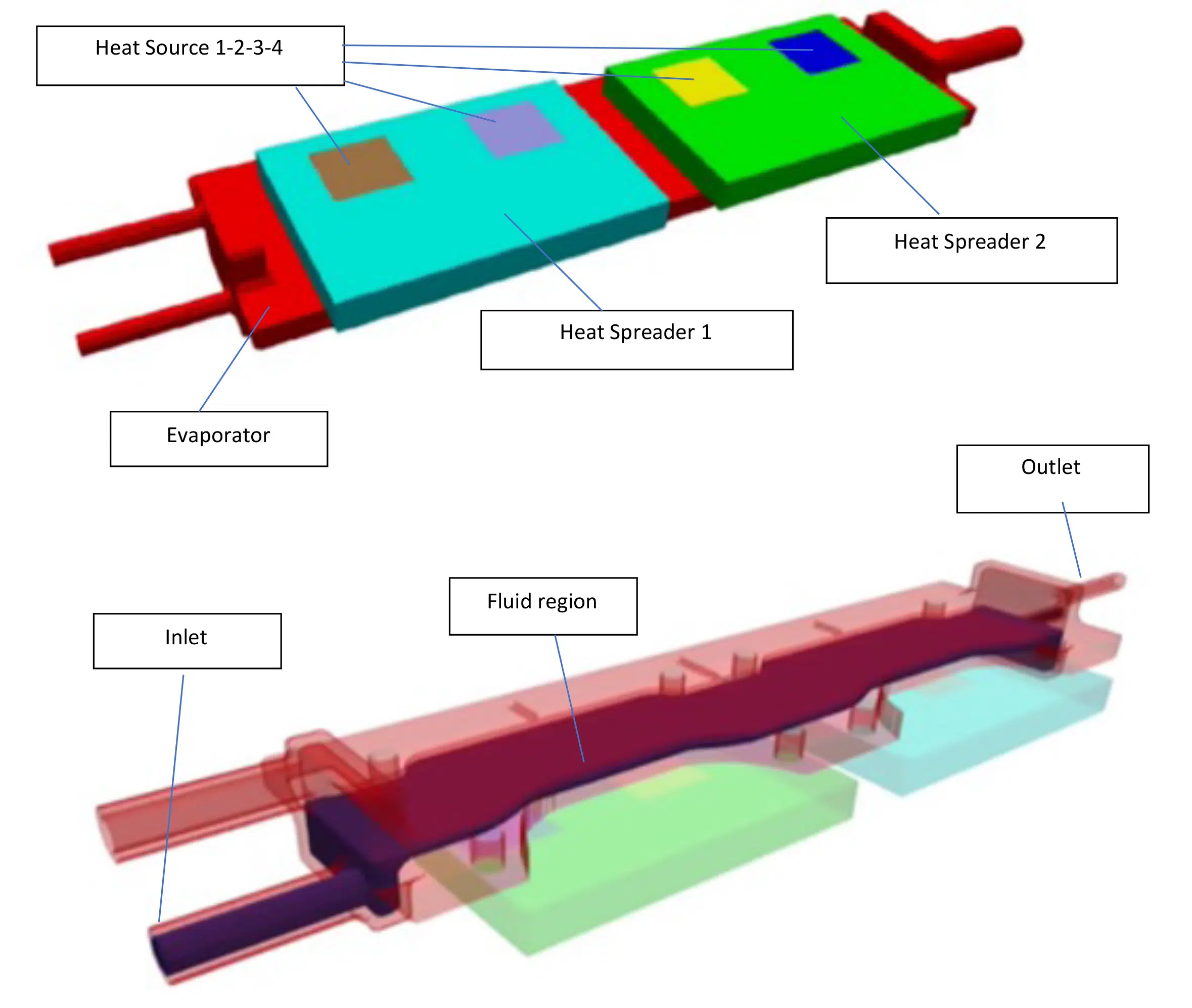
To demonstrate the feasibility of the proposed design approach, the remainder of the article is dedicated to a case study. The base geometry, shown in Figure: 1, represents a simplified 2-phase cooled heat sink, called the evaporator, that could potentially be used in actively cooled communication satellites. The goal of the study was to minimize the temperature on the heat sources (Equation 2), within a pressure drop constraint (Equation 3), and additional manufacturing constraints for 3D printing.
min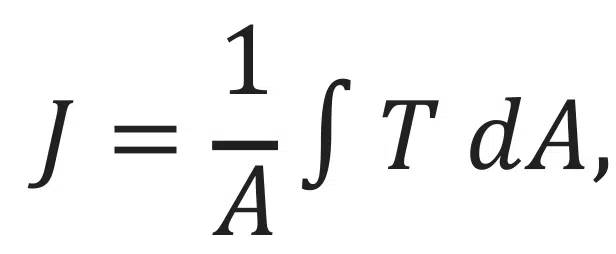
subject to 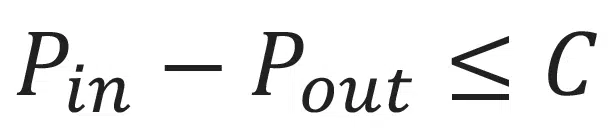
Figure 1: base geometry for the design optimization study
The base geometry for the optimization study is shown in Figure 1. The geometry consists of 4 heat sources that are mounted on two heat spreaders. In turn, the heat spreaders are mounted on the evaporator. For the numerical analysis, the geometry was discretized using a fully hexagonal mesh.
The heat spreaders and the evaporator are both manufactured from aluminum alloys (AL 6061) with a density of 2701 kg/m³ and thermal conductivity of 150 W/mK. A contact conductance of 30 kW/m²K is applied at the interface between the heat spreaders and the evaporator. A total heat dissipation rate of 200W, i.e. 50W per heat source, is imposed. Saturated ammonia is used as the coolant with inlet conditions of 80°C and pressure of 41.42 bar. The properties of ammonia under these conditions are given in Table 3. The vapor quality at the inlet is set to 6.7e-5 (or a vapor fraction of 0.1%). The mass flow rate equals 3.33e-4 kg/s. Under these conditions, the quality increases up to 0.6865 at the outlet.
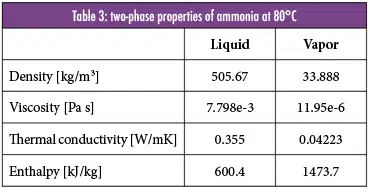
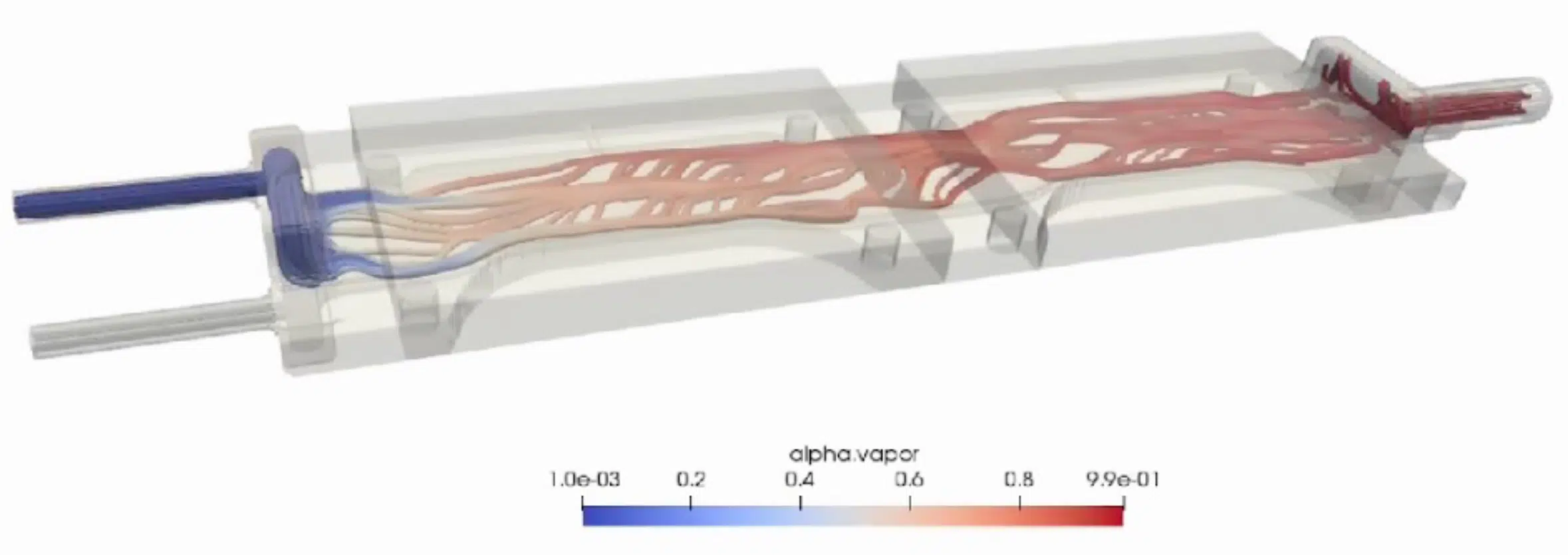
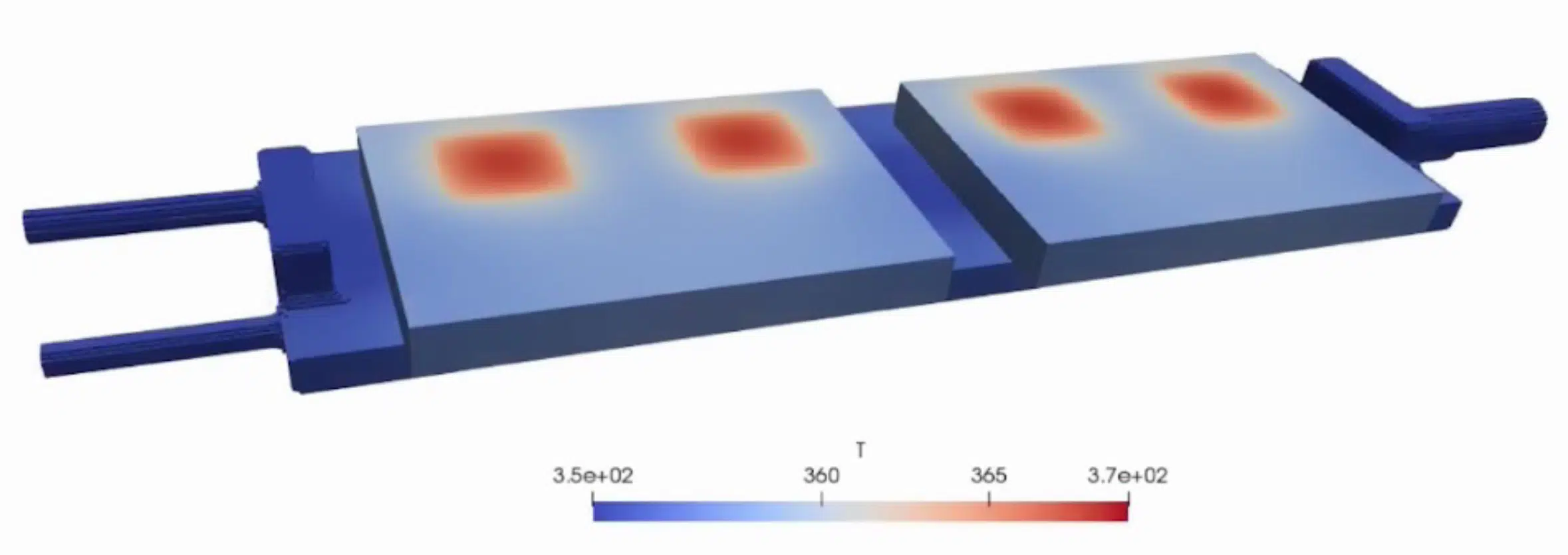
Figure 2: AI design with (a) alpha.vapor the local vapor fraction; (b) evaporator temperature.
The final design is shown in Figure 2 (a) in which the fluid channels are colored according to the local vapor fraction. The evolution of the temperature is shown in Figure 2(b). The optimization searches for a balance between low and high heat transfer in large and small channels at the cost of a low and high-pressure drop. This explains why the design is different under each cooling cell: there is a difference between the fluid entering the regions below each cooling cell, and a difference in flow properties such as density, quality, and viscosity, which all affect the pressure drop. To evaluate the performance of this component and the effectiveness of the optimization, the evaporator was built and tested under laboratory conditions that demonstrated a 15% performance increase compared to a conventional design, constructed from a series of parallel channels (see Figure 10 in [3] for the design). The experimental analyses were performed by the NLR institute, see [3] for more details on the experimental setup and the test procedures.
Conclusion
This work demonstrates that generative design can be used to design a two-phase evaporator cooling system with minimal human input or interaction. A fully three-dimensional solid and fluid domain model, combined with an advanced interface heat transfer model based on a two-phase multiplier concept, was used to accurately model the physical behavior of the system. A case study demonstrated that the cooling could be improved up to 15% without affecting pressure drop, manufacturing cost, or cost of the device.
Acknowledgments
The work presented was carried out in close cooperation with AVS, Airbus Defence and Space, CEA, CERN, and NLR. It has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 822027. This publication reflects the author’s view. The European Union’s Horizon 2020 research and innovation programme is not responsible for any use that may be made of the information.
References
[1] Maqbool, M.H., 2012. Flow boiling of ammonia and propane in mini channels (Doctoral dissertation, KTH Royal Institute of Technology).
[2] Diabatix ColdStream©, https://coldstream.diabatix.com
[3] Van Gerner, H.J., 2021. Preliminary design of a mechanically pumped cooling system for active antennae, 50th International Conference on Environmental Systems, ICES-2021-002.
[4] Todreas, N.E. and Kazimi, M.S., 2021. Nuclear systems volume I: Thermal hydraulic fundamentals. CRC press.
[5] Ghiaasiaan, S. M., 2008, “Two-phase flow, boiling, and condensation.” Conventional and miniature systems