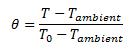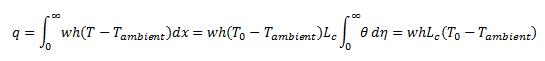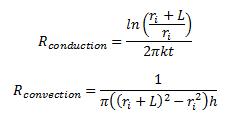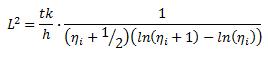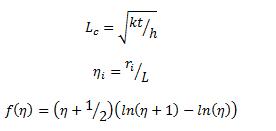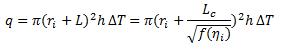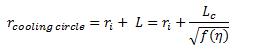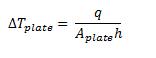Introduction
One of the most baffling things in cooling for the novice mechanical engineer is the fact that with the exact same geometries and dimensions, thermal solutions just do not perform the same. Past results do not guarantee future performance, and doubling the surface area of a tried and tested design to double the cooling capacity, as per Newton’s cooling law, does not work out in any predictable way.
Why is the thermal world so unpredictable? The success of a thermal design depends on more than just mechanical dimensions or material properties. Heat and temperature are invisible, and as 75% of the human cortex is devoted to processing visual information, the way that thermal designs work is not intuitively clear at gut level. This article is an effort to make heat spreading, one of the most important mechanisms in electronics cooling, more visual and thereby more intuitive, by use of the Cooling Circle.
The importance of heat spreading
Consider the heat loss from convective cooling, which is proportional to the product of heat transfer coefficient h, area A and the temperature difference between the surface area and the constant ambient, T. Now imagine a surface with non-uniform temperature, and a surface plot of this temperature distribution relative to ambient. A surface area segment dA, at temperature T has a convective heat loss of h(T- Tambient)dA, and the total convective heat loss is the sum of all the segments, or the integral dA. In other words, if we make a plot of the temperature difference between the surface temperature and the ambient, heat loss is h times the volume below the temperature surface. This means that heat behaves like a volume of water: A volume of water in a tall glass has a high water level. The same volume of water in a wide glass has a low water level. Likewise, if a given amount of heat has a steep temperature profile, corresponding to little heat spreading, the maximum temperature will be high. The same amount of heat with a flatter temperature profile, corresponding to more heat spreading, results in a lower maximum temperature, because the volume below the steep and the flat temperature surface is equal.
Figure 1: at the same power, more heat spreading results in lower source temperatures.
In electronics cooling it is key to accommodate a certain heat dissipation while keeping the heat source below a certain temperature. In terms of the water analogy, this means that the amount of water is given, and the water level is given. The thermal engineer’s job boils down to providing sufficient area and sufficient heat spreading. The area is visible, and the purpose of this paper is to visualize the heat spreading.
A note on thinness
This paper is about heat spreading in a thin plate, meaning that the geometry is so thin that there are no significant temperature differences between both sides of the plate. It follows that it does not make a difference whether the source is on top of the board, embedded in the board, or on the bottom of the board or heat sink. Furthermore, it does not matter if the cooling is on the top of the plate, on the bottom of the plate, or both. In a very thin geometry, only the total combined heat transfer coefficient is relevant. A plate is thin if t<10% k/h or in other words, if the Biot number Bi<0.1 [1]. When this is not the case, please consult references [5,6] for more information on this topic.
Rectangular thin fin, Characteristic Length
Consider heat spreading along a flat rectangular thin fin, of width w, thickness t and thermal conductivity k. One edge of the fin is heated, with T(x=0)= T0. The fin conducts heat along its length, and loses heat to the ambient by convection, at heat transfer coefficient, h. The temperature along the fin scales with the prescribed end temperature and the ambient temperature [1-3]
The coordinate along the fin scales with a length scale, Lc. This length scale follows directly from the governing differential equation [3], but it also emerges as the length for which the thermal resistances for conduction and convection are equal [1]:
By definition the scaling length Lc is the characteristic length
For infinitely long rectangular fins [1]
In other words: the temperature decays exponentially with rate 1 from θ=1 at η=0, to θ=0. In exponential decay, the influence of the imposed end temperature continues indefinitely but in practice, the influence diminishes fast: At η=1, θ=0.37; at η=2, θ=0.14, and at η=3, θ=0.05. Less than 5% of the imposed temperature is found beyond a distance of 3Lc. Furthermore, since the area below the exponential curve is finite and equal to 1, the total heat lost to the ambient is finite as well, and given by
This shows the infinitely long rectangular fin with T0 imposed at the end x=0, experiences heat loss to the ambient as if a length Lc is heated to T0, and the remainder of the fin stays cold. Since the temperature is uniform over the width w of the fin, this heat represents the volume of a block of length Lc, width w and height T0., equal to the loss of a linear temperature drop from To to ambient over a distance of 2Lc. It follows that a linear temperature drop over distance 2Lc is a good approximation for the exponential decay.
The exponential decay of temperature from the heated edge explains why increasing the surface area of a cooling fin does not always improve thermal performance. If a fin is much shorter than Lc, doubling the length for instance from 0.1 Lc to 0.2 Lc will indeed roughly double the cooling capacity since the added length will be heated. If the fin is about 1 Lc long or more, increasing the fin length will not help that much, as the fin is already experiencing a significant temperature drop from the base to its tip, and therefore added material will remain unheated In that case, using a thicker fin or a better conducting material will help to heat the exisiting surface area and thus improve cooling.
Cooling circle for large sources
Heat spreading from the edge of a relatively large round source outwards resembles heat spreading of the rectangular fin discussed above. Thus, the rectangular thin fin theory extends to large circular sources on an infinitely large thin plate. If we assume the source is isothermal, the source and the edge will both be at temperature T0. Instead of the rectangular fin length Lc, there will be a Lc wide ring extending from the source edge. The total heat loss is the loss of the source itself plus the additional loss from the heated ring around it. In other words, the circular source cools as if it has a radius (ri+Lc) at temperature T0. We define the circle with radius Ri+Lc as the cooling circle.
Again, the cooling circle explains why sometimes enlarging a heat sink works and sometimes not. For a flat plate that is well inside the cooling circle, increasing the size will correspond to increased thermal performance since the added surface area is heated. In contrast, increasing the size of a plate which is already much larger than the cooling circle will not work, just like the case of the rectangular fin.
IR pictures show that at some distance, the heated zone around a square heat source is circular in shape. Therefore, the circular source approximation is applicable to a wide range of non-circular source shapes.
Cooling circle for Small sources
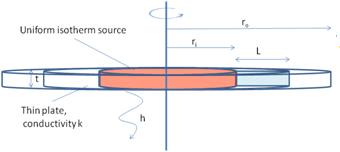
Figure 2: Circular geometry
When sources become relatively small the temperature will drop off more than exponentially: heat flowing out radially from a small source passes through successively larger and larger circles, and, in terms of the water analogy, it is spread thinner and thinner.
Consider the geometry in Figure 2: a circular heat source with radius ri on a thin plate, thickness t, thermal conductivity k, cooled with heat transfer coefficient h.
Assuming heat spreads out radially over a distance L from the edge of the source, the thermal resistances are:
Equating the resistances and defining
leads, after some re-arranging, to
Again, the characteristic length Lc emerges, but it is accompanied by a correction function f, depending on the relative size of the source ηi
The correction function incorporates the source size effect. For η >0.5 the factor is about 1, which aligns with the result for large sources.
Figure 3: correction factor
The temperature solution to heat spreading on the plate is well known as the solution for an annular thin fin with an imposed temperature T0 on the inside edge. This solution is expressed in Bessel functions, The reader interested in the mathematical background is advised to consult references [2-4], this article presents only the final results.
For the large circular source on the infinite thin plate, cooling is as if the source had the Characteristic Length added to the radius:
This suggests that the new length scale can be used in the same manner.
A spreadsheet calculation confirms that indeed this is a good approximation over a large range of ηi.
Figure 5 shows that the “cooling circle” heat loss approaches the analytical solution using Bessel functions to within 6%.
A circular source on an infinite plate cools with a cooling circle with radius
How far does the heat go?
So far, we have derived that a circular heat source on an infinite plate cools as if it had the area of the cooling circle. But when is the plate infinite?
Figure 4: Temperature surfaces
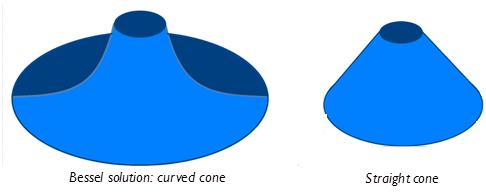
In the case of the rectangular fin it was shown that a straight line over a distance 2Lc replaced the curved exponential temperature drop. Expansion to the circular domain points to replacing the curved cone from the Bessel solution with a straight cone, with a temperature drop over 2Lc, as shown in Figure 4. For small sources, the linear drop will be steeper for the reasons discussed before. In the limit to vanishingly small sources, the linear drop extends over √3L with L=Lc/√(f(ηi) [4].
Figure 5 shows L/Lc and the % difference between the heat loss according to the Bessel solution and the cooling circle for finite plates with rims ranging from 1 L to 10 L around the source. The difference is defined as (CC (Cooling Circle) value – Bessel value)/Bessel value * 100%.
The cooling circle value is always assuming that there is an infinite plate, so it is only a function of the source radius. The Bessel value includes both the source size and the plate size. For sufficiently large plates the comparison illustrates the validity of the cooling circle approach. For the exponential temperature drop it was seen that any distance above 3L could be considered about “infinite”. The curves for +5L and +10L coincide, confirming these are the “infinite” values. These comparison shows that for infinite plates, using the cooling circle is accurate to within 6%.
Figure 5: L/Lc and CC vs Bessel heat loss
For smaller finite plates the comparison between the Bessel value and the cooling circle value is an indication of how much heat loss is realized on the smaller finite surface. The curves for rout = rin + √3 L and rout = rin + 2 L show that 75% – 85% of the total heat loss takes place in the source and the √3 L cq 2 L wide ring around it, which aligns well the linear temperature drop over 2Lc for large sources and √3L for vanishingly small sources.
The rim = L curve is the curve where the finite plate is the exact size of the cooling circle. This curve shows that in case of large sources, ri ≥ Lc, 70% or more of the total heat transfer takes place within the cooling circle itself. For small sources this is not the case: for sources with ri ≤ 0.01 Lc less than 25% of the total heat transfer takes place in the cooling circle itself. The heat loss “as if the cooling circle is at a uniform temperature” is the result of a uniform temperature plateau at the source itself added to a the heat loss from a temperature drop extending over a distance of √3L to 2L around the source. With the small source area, the additional heat loss is in fact dominant over the heat loss from the source itself.
Figure 6: Plate size and Cooling circle
If a plate is larger than √3L to 2L around the source then the plate is about infinite, and the cooling of the source goes with the cooling circle.
If a plate is much smaller, cooling of the source is determined by the plate area:
The linearized rectangular fin case can be used to construct a somewhat better approximation to the source temperature rise. In the rectangular case the average plate temperature corresponds to the halfway location between source and plate edge, and it is known that the temperature drops to ambient over 2L distance. This fixates the slope and enables calculating the source temperature as
For a better approximation the reader is invited to consult [4].
Application Example
As an example, the case of a 3x3x2 mm well-conducting heat source on a 100x100x1 mm vertical plate, cooled by h=10 W/m2K on both sides of the plate will be calculated. In one case, the plate is made of ceramic, k=1 W/mK, and in the other case the plate is made of an aluminum alloy, k=160 W/mK.
|
t |
k |
h |
Lc |
Bi |
|
| case |
mm |
W/mK |
W/m2K |
mm |
– |
| aluminum |
1 |
160 |
20 |
89 |
0.000125 |
| ceramic |
1 |
1 |
20 |
7.1 |
0.02 |
Table 1: calculate Lc and Bi
Table 1 shows the calculated Lc and Bi .The results show that for both cases, Bi < 0.1 so the plate is thin and the cooling circle is applicable.
|
case |
ri |
rout |
rout-ri |
Lc |
ηi =Ri/Lc |
f(ηi) |
L |
|
mm |
mm |
mm |
mm |
mm |
|||
|
aluminium |
1.7 |
56 |
55 |
89 |
0.019 |
2.1 |
62.2 |
|
ceramic |
1.7 |
56 |
55 |
7 |
0.239 |
1.2 |
6.4 |
Table 2: correction factor, L and the distance between the source and the edge of the plate
a. Ceramic plate
The rim around the component (55 mm) is much larger than 2L (2 x 6.4 mm). Therefore the plate is infinite, we have a hotspot situation. The component on the ceramic plate cools with the cooling circle with radius ri + L=1.7 + 6.4 = 8.1 mm, area 206 mm2
With a dissipation of 1 W and 35 °C ambient, the component temperature will be 278 °C
b. Aluminum plate
The rim around the component is less than L wide so the plate is inside the cooling circle. The component on the aluminum plate cools with the plate area: A=0.01 m2.
With a dissipation of 1 W and 35 °C ambient, the average plate temperature will be 40 °C.
The source will be 40 – 41.5 C.
c. Comparison to Numerical results
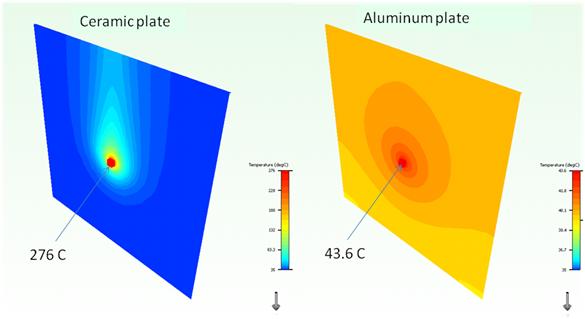
Figure 7: numerical results
The temperature fields from numerical simulations confirm that for the ceramic plate, the cooling circle is entirely on the plate, and the edge is at ambient temperature. Also it is confirmed that for the aluminum plate, the entire plate is heated. Source temperatures and Rth are align well with the cooling circle results, as is shown in Table 3
|
Source Temperature (°C) |
Rth (K/W) |
|||
|
cooling circle |
numerical |
cooling circle |
numerical |
|
|
ceramic |
278 |
276 |
242 |
241 |
|
aluminum |
40 – 41.5 |
44 |
5 – 6.5 |
8.6 |
Table 3: comparison to numerical results
References
- Luiten, W., “Heat spreading in a thin rectangular fin”, submitted to Therminic 18, Budapest, 2012
- Wong, H. Y., “Heat transfer for engineers”, Longman, London, 1977
- Luiten, W., “Characteristic length and cooling circle”, Semitherm 26, San Jose 2010
- Luiten, W., “Heat spreading from a small source on a thin plate”, Semitherm 28, San Jose 2012
- Lasance C., “Heat spreading: not a trivial problem,” ElectronicsCooling, Vol. 14, May issue, pp. 24-30, 2008
- Lasance C., “How to estimate heat spreading effects in practice,” J. Electron. Packag., 132, 031004, 2010
Wendy Luiten is a senior thermal specialist at Philips Research in Eindhoven. She has 25+ years experience in the thermal and mechanical field and 15+ years experience in cooling Consumer Electronics products. She is also lecturer at Electronics Cooling courses, and has lectured over 15 times in Asia, US and Europe. She has authored numerous papers, and holds 4 patents. She received the best paper award at Semi-Therm 2002 and is a member of the Semi-Therm and Therminic program committee. Wendy Luiten received a MSc in mechanical engineering (heat & fluid flow) from Twente Technical University, the Netherlands.