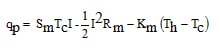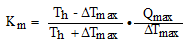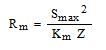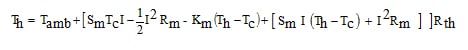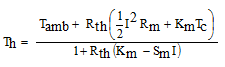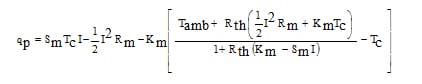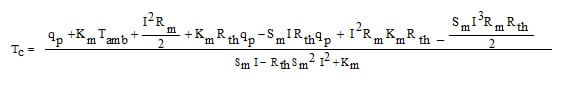The application of thermoelectric devices to cool electronic components has been of interest to thermal engineers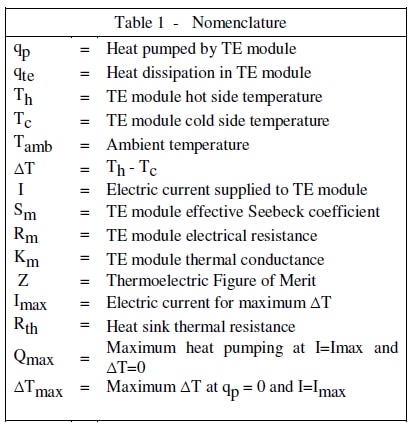
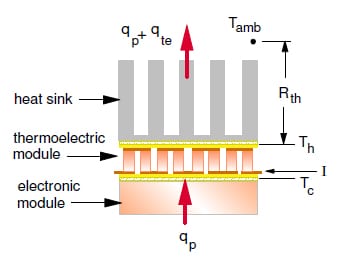
Figure 1 provides a typical example of a TE module cooling application. In this application, a TE cooling module is sandwiched between an electronic module dissipating heat and a heat sink rejecting heat to the cooling air. By passing electric current through the TE module in the appropriate direction, the side attached to the electronic module (Tc) becomes cooler, lowering the temperature of the component, and the side attached to the heat sink (Th) becomes warmer, providing a greater temperature difference for heat rejection to ambient (Tamb). In effect, the TE module “electronically” pumps the heat (qp) dissipated by the component from the cold side to the hot side of the TE module. Of course nothing is free and the penalty that must be paid in this case is the Joule heating (qte) that takes place as current flows through the array of thermoelectric couples comprising the TE module. It should be noted at this point that, for steady-state operation, the heat pumped by the TE module must be equal to the heat dissipated by the electronic component being cooled and the heat rejected to the cooling fluid by the heat sink will be equal to the sum of the heat pumped by the TE module and the Joule heating within the TE module.
In an earlier article, Luo [5] presented the following equations for heat pumping with a thermoelectric cooling module
(1)
and the corresponding TE heat dissipation
(2)
in terms of the module parameters defined in the nomenclature. In addition to the above two thermoelectric equations we have the following heat transfer equations relating the TE module hot side temperature to the temperature of the ambient cooling fluid
(3)
where Rth is the heat sink thermal resistance from base to ambient. For the purposes of the calculations in this article, I have chosen to neglect the thermal interface material (TIM) resistance between the hot side of the TE module and the base of the heat sink, so that the temperatures at the hot side of the TE module and the base of the heat sink are the same.
Before these equations can be applied to a specific TE module it is necessary to know the values of the TE module parameters Sm, Rm, and Km. These values are not provided by TE module vendors, instead vendor data sheets will usually provide the values of Qmax, Imax and ΔTmax at a specified hot side temperature. However, Luo’s article developed equations which may be used to obtain the necessary TE module parameters from vendor data. These equations are as follows:
(4)
(5)
(6)
(7)
It is important to note that in these equations, and in the equations to follow, all temperatures are in Kelvin temperature units (i.e., Kelvin temperature = Centigrade temperature + 273.16).
Luo used equations (4-7) to determine the module parameters for actual vendor TE modules and then input values of I, Th, Tc and Tamb in equations (1-3) to obtain values of qp, qte, and Rhs for comparison with values obtained from vendor software. However when considering an actual application, the value of Th is not known a priori. Typically what is known, is the allowable component surface temperature and the expected heat dissipation of the component. So, we would like an expression relating the heat pumped by the selected TE module to a specified cold side temperature, TE current and module parameters, the heat sink thermal resistance and the ambient fluid temperature. We would also like an expression relating the TE module cold side temperature to the heat pumped, TE current and module parameters, the heat sink thermal resistance and the ambient fluid temperature. The desired relationships may be obtained using equations (1-3) and a little algebra.
Substituting equations (1) and (2) into equation (3) we obtain,
(8)
and then solving this equation for Th we obtain,
(9)
which may then be substituted into equation (1) to obtain equation (10) for qp as a function of the specified cold temperature, Tc
(10)
Alternatively, equation (10) may be rearranged to solve for Tc as a function of the heat pumped, qp, which as noted earlier equals the component heat load,
(11)
An example of the application of equation (11) follows. In this example we will consider a 40 mm x 40 mm electronic module with a heat dissipation of 40 W. Accordingly, a 40 mm x 40 mm thermoelectric module is chosen to be secured between the top of the electronic module and the base of the heat sink. The published vendor data for the selected TE module are:
Qmax = 83.9 W
ΔTmax = 72oC
Imax = 6.7 A
Using the above values in equations (4-7) the required TE module parameters are determined to be:
Sm = 0.068 V/K
Km = 0.712 W/K
Z = 0.002815 1/K
Rm = 0.068 Ω
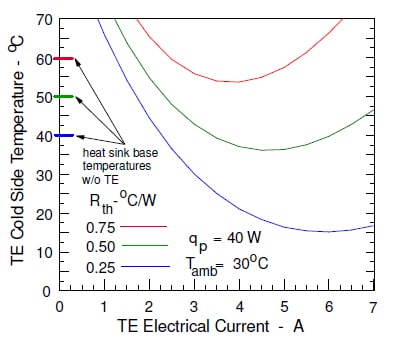
These values are then used in equation (11) to generate values of TE cold side temperature for a range of TE electric current values, three different values of heat sink thermal resistance (i.e., 0.25, 0.50 and 0.75oC/W) and a cooling fluid temperature of 30oC. The results of these calculations are shown in Figure 2, illustrating the benefit derived by using a TE module for this application. For example, the minimum cold side temperatures of 53.6, 36.2 and 15.2oC obtained with the TE module-heat sink combination compare quite favorably to the heat sink base temperatures of 60.0, 50.0 and 40.0oC obtained with the heat sink alone.
These results also illustrate the typical behavior at the cold side of a TE module as the electric current is increased. Initially increasing current results in lower cold side temperatures until a minimum cold side temperature is reached. After that minimum value, Joule heating will become the predominant factor and further increases in current will result in increases in cold side temperature. It may also be seen that decreasing the heat sink thermal resistance makes it possible to take advantage of increased current to achieve lower TE module cold side temperatures before the cold side temperature rises with increased current.
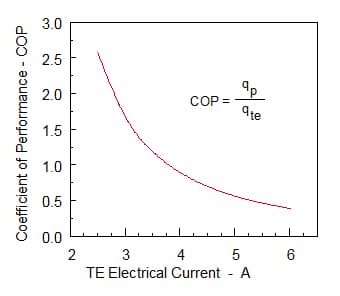
Another important consideration when using TE modules is the electrical power that must be supplied to achieve the desired cooling effect. A relative measure of this is the COP or Coefficient of Performance. Some readers may recall the definition of COP from their undergraduate thermodynamics course, which is the ratio of heat transferred to the work input. In this case the COP of a thermoelectric cooling module is the ratio of qp in equation (1) to qte in equation (2). COP as a function of electric current for the present example is shown in Figure 3. Although a slightly different COP curve resulted for each of the three heat sink thermal resistances considered, the differences were so small that only one curve is shown (i.e., for Rth = 0.25oC/W). Since the heat pumped in all cases is equal to the component heat load of 40 W, the COPs in Figure 3 indicate that the amount of power required for the TE module varies from 15.5 W at 2.5 amps to 102 W at 6 amps.
As was noted earlier, the TIM thermal resistance between the base of the heat sink and the TE cooling module was ignored in this example. However, the effect of TIM thermal resistance can easily be accounted for using the preceding equations. To account for the increase in the TE hot side and cold side temperature, the TIM thermal resistance between the TE cooler and the base of the heat sink is added to the value of the heat sink thermal resistance used in equations (10) and (11). As an example, if we consider a TIM area thermal resistance of 10oC-mm2/W, the TIM thermal resistance for the 40 mm x 40 mm module considered in the preceding example would add 0.0063oC/W to the external thermal resistance. Using a heat sink thermal resistance of 0.256 in equation (11), the minimum achievable cold side temperature of 15.2oC shown in Figure 2 would become 15.8oC.
The equations presented here should provide a useful tool for an early estimate of whether or not a particular TE module may provide useful cooling enhancement. However, the reader is cautioned to remember that these equations may not be expected to provide exact results. Inherent in the equations and derivations presented is the underlying assumption that the thermal and electrical properties of the TE module are constant, which is certainly not the case. For example, Luo’s [5] comparisons with vendor’s software results showed differences in predicted heat pumping values of 3 to 11%. It is expected that similar uncertainties can exist in the method presented here.
REFERENCES
Godfrey, S., “An Introduction to Thermoelectric Coolers,” Electronics Cooling, September 1996.
Simons, R.E., “Application of Thermoelectric Coolers for Module Cooling Enhancement,” Electronics Cooling, May 2003.
Johnson, D.W., and Bierschenk, J., “Latest Developments in Thermoelectrically Enhanced Heat Sinks,” Electronics Cooling, August 2005.
Simons, R.E., “Effect of Improved Thermoelectric ZTs on Electronic Module Coolability,” Electronics Cooling, November 2006.
Luo, Z., “A Simple Method to Estimate the Physical Characteristics of a Thermoelectric Cooler from Vendor Datasheets,” Electronics Cooling, August 2008.