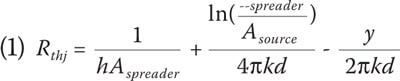Author
Clemens J.M. Lasance, Guest Editor
Fact: many papers discussing LED thermal management issues report values of about 100 W/cm2 and use the same arguments that are valid for ICs to demonstrate that some critical value has been reached. The question to be addressed: is this indeed a fact, or can it be shown to be a fairy tale, and hence do we need different arguments to judge LEDs and ICs?
Let us start with a convincing example. Suppose we compare the two following cases for liquid cooling:
They differ only in the source and spreader areas, keeping the heat flux constant.
The next table shows the results for both the average and maximum temperature of the sources:
The values are calculated using the heat spreader equations derived by Song, Lee and Au [1].
What do the results tell us? Two significant facts.
Firstly, the larger the source, the larger the temperature difference between the average and the maximum temperature (this is, by the way, an important drawback of the very useful web-based calculator by the U. of Waterloo [2] that only presents the average temperature over the source). The problem is caused by the fact that we are dealing with increasing temperature gradients over the surface when the area increases with respect to the source.
Secondly, the maximum temperature of the smaller source with the same heat flux results in a temperature drop of more than a factor of 5. How these values are related can best be observed by taking a look at the L-equation [3,4,5] that can be used over a quite large range of practical applications but is not as accurate as the SLA-equations:
The first term can be considered a convection term, the second a conduction term and the third a correction term. It is easy to see why the temperature goes down when the area ratio is kept constant. Only the first term changes, and in our case the conduction term is much larger than the convection term for the larger source (indicates negligible heat spreading), and much smaller for the smaller source (indicates significant heat spreading). Simply put: the heat fluxes do not scale when only the areas are changed while keeping the area ratio constant. In order to scale correctly, the product k*d should also be scaled, meaning in this case that the thickness should be reduced by a factor of 100 for the smaller source to result in the same temperature rise keeping the flux constant. Because this is never the case in practice due to the fact that the PCB or submount is more or less fixed, we cannot compare critical heat fluxes without mentioning at least the source area. In closing this example, let us compare the critical heat flux that corresponds with a maximum temperature rise of 60 °C for both cases.
The big difference is noteworthy, and boils down to the following: what is called a critical heat flux for ICs is not per se critical for LEDs.
You may wonder why people always talk W/cm2. The reason is that the thermal management field has been dominated by the cooling of processors that have dissipating areas of order (cm2).
How to prevent these misunderstandings? First, designers should be aware of the problem. A useful rule of thumb has been formulated by Wilcoxon and Cornelius [6] using the following equation showing the relation between a critical flux and the source area:
Its use is limited to areas larger than about 0.1*0.1 mm2 being only a problem for applications involving very small sources . It should also be realized that this limit is only a very rough estimate and depends not only on the source size but also on the spreader thickness, area, thermal conductivity and boundary conditions.
What every designer should do who is being confronted with heat spreading is to use spreadsheet software with the SLA equations, in such a way that h and k are considered parameters. It is then easy to get enough data in a couple of minutes to construct useful graphs.
Conclusion
It is important to understand that it does not make sense to use the same heat flux limits for both processors and LEDs alike, and I propose to authors dealing with high-power LED applications to refrain from mentioning e.g. 100W/cm2 as a critical value above which liquid cooling should be used, based on IC-related data. Instead, I suggest to quote the ‘raw’ data related to the size of the source, e.g. for a junction W/μm2, for an LED W/mm2, for a die W/cm2, for a TV backplane or a large LED luminary W/m2.
References
[1] Song S., Lee S. and Au V., Closed-Form Equations for Thermal Constriction/Spreading Resistances with Variable Resistance Boundary Condition, IEPS Conference, pp. 111-121 (1994)
[2] MHTL Simulation Tools. 2012. MHTL Simulation Tools. [ONLINE] Available at: http://mhtlab.uwaterloo.ca/RScalculators.html
[3] Lasance C., Heat spreading: not a trivial problem, ElectronicsCooling, Vol. 14, May issue, pp. 24-30 (2008)
[4] Lasance C., How to Estimate Heat Spreading Effects in Practice, J. Electron. Packag., 132, 031004, (2010)
[5] Lasance C., Two-layer heat spreading approximations revisited, Proc. 28th Semitherm, San Jose, CA, 2012
[6] Wilcoxon R. and Cornelius D., Thermal management of an LED light engine for airborne applications, Proc. Semitherm 22, Dallas, pp.178-185 (2006)