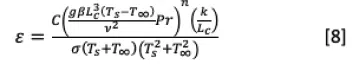Introduction
This is the first installment in a series of articles that aim to explore a range of practical topics on radiation that will be relevant to those of us focused on electronics cooling and thermal design.
While radiation is one of the three fundamental modes of heat transfer, it is often the last topic covered in an introductory heat transfer course. This may leave some of us intimidated when we look back at the complicated equations, try and remember the various definitions, decode the underlying assumptions, etc. I hope to bring some clarity to these common radiation questions here.
Let’s start with the most basic question. When do we need to consider radiation in thermal design, and when can it be reasonably neglected? Understanding this is useful because radiation is a complex phenomenon, introduces non-linearities, and can be computationally expensive to calculate (e.g., non-linear, view factors, ray tracing, etc.).
The Basics
For a gray body, the net heat crossing the surface of the body is defined by equation 1; where Q is the heat rate in Watts, ε12 is the effective emissivity between the surface and an interacting body, F12 is the view factor between the surface and a interacting body, A is the surface area, σ is the Stefan Boltzmann constant (5.67e-8 W/m2-K4), Ts is the surface temperature of the body in K, and T∞ is the temperature of the interacting body in K.
Q=ε12F12Aσ(T4s−T4∞) [1]
Inspection of this equation identifies the key factors influencing radiative transfer. The emissivity, view factor and surface area represent linear design ‘knobs’ that influence heat rate. The temperature term is non-linear and increases to the 4th power.
Given that conduction and convection are linear functions of the temperature difference, it is also often convenient to reformulate the radiation equation into the linearized format provided by equations 2 and 3, where hr is a linearized radiation heat transfer coefficient.
Q=hrA(T s−T ∞) [2]
For the purposes of this study, we will assume that the surface of interest interacts with a blackbody (ε =1) that fully surrounds it (F12=1). This approximates a surface that is radiating to a uniform environment, simplifying equation 3 to equation 4. See reference [5] for additional information on the derivation of this equation.
These equations now equip us with the tools needed to quantify the importance of radiation across common thermal applications.
Natural Convection Environments
Let’s start by quantifying when radiation is important in natural convection environments. Natural convection environments are common for passively cooled devices such as consumer electronics products. The empirical Nusselt correlation for natural convection is re-arranged to provide the convection coefficient (hc) in equation 5, where, Ra is the Rayleigh number, k is the thermal conductivity of fluid medium, and Lc is the characteristic length of the body, and C and n are empirical constants. For the purposes of this article, we will assume a vertical plate with coefficients C and n of 0.59 and 0.25 respectively [1]. However, one can easily plug in different correlations for varying geometries and/or orientations.
The Rayleigh number is calculated with equation 6, where g is the acceleration of gravity, β is expansion coefficient, v is kinematic viscosity, and Pr is the Prandtl number.
The heat balance for a device can be calculated by equating its heat generation rate with the sum of the heat rejected by natural convection and radiation as shown in equation 7.
Q= (hr + hc)A(Ts − T∞) [7]
For the purposes of determining when radiation matters, it is convenient to equate the natural convection and radiative heat transfer coefficients and solve for one of the common design variables. In this case, we will solve for the emissivity required to match the heat rejected by radiation and natural convection, see equation 8.
Although this equation is a function of many variables, the characteristic length and the temperature are of greatest interest because they represent thermal design knobs.
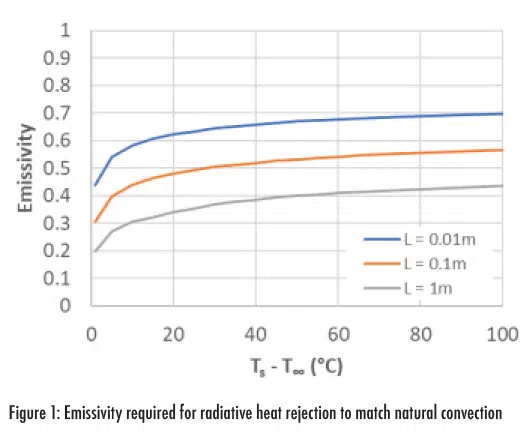
Figure 1 confirms that radiation matters and must be considered in natural convection environments. The emissivities of common external painted surfaces are typically ≥ 0.8. This means that radiation may be the dominant heat rejection mode across device length scales and temperature ranges in natural convection environments. Even for the reasonably low emissivity of 0.2, which may be representative of a polished surface, radiation cannot be ignored.
Forced Convection Environments
Does the importance of radiation extend to forced convection environments? Forced airflow is a common means to actively cool electronics such as laptops or data centers. It can consist of internally ducted airflow, or external airflow over a product. This airflow may be intentionally applied using a fan or can naturally occur via wind or movement. The empirical correlation for the average external forced convection heat transfer coefficient is provided in equation 9, where ReL is the Reynolds number calculated at the characteristic length, and C, m A and n are empirical constants. We will assume a flat plate with the coefficients C, m, A and n of 0.037, 0.8, 871 and 0.33 respectively for mixed flow and 0.664, 0.5, 0 and 0.33 for laminar flow, with turbulent transition at a Reynolds number of 5×105 [1]. However, one could similarly expand to other geometries and conditions by considering alternate correlations.
The ratio of the radiative heat rejection to the total heat rejection in forced convection scenarios is illustrated in Figure 2. In order to represent typical electronics cooling scenarios, the surface temperature is assumed to be 50°C, the ambient environment is assumed to be 25°C, and the surface emissivity is assumed to be 0.8.
Radiation is shown to be important only for small Reynolds numbers (velocities < 5 m/s) or for very large body dimensions. The Reynolds number dependence makes sense, and at very low Reynolds numbers the flow velocities may approach those of natural convection. The non-negligible radiative contribution to cooling of large bodies is due to the increased boundary layer thickness that yields a reduced average convection coefficient. Note that this assumes parallel flow along a flat plate with no obstructions. Flow impingement and complex flow structures typical of complex real-world geometries will generally increase convective mixing and further reduce the effect of radiation. Thus, radiation can often be neglected in electronics cooling with forced convection. However, one should double check when the application includes low velocities or large geometrical dimensions.
Aerodynamic Heating Environments
While it is common for both radiation and convection to represent a means for rejecting heat in many electronics cooling applications, radiation also plays an important role in some less common electronics cooling applications. One such application occurs in high-speed vehicles that experience aerodynamic heating. In these applications, convection can represent a heat source to the electronics. The convective heat flux is driven by the recovery temperature (Tr) as illustrated in equation 10. The recovery temperature is calculated using equation 11 and is a function of the Mach number (M), the recovery factor (r), and the heat capacity ratio (γ).
Qc= hcA(Ts − Tr) [10]
When convection acts as a heat source instead of a heat sink, radiation will be a primary means of rejecting heat to cool the electronics. The equilibrium surface temperature of a body experiencing aerodynamic heating can be determined by balancing equations 1 and 10, resulting in equation 12.
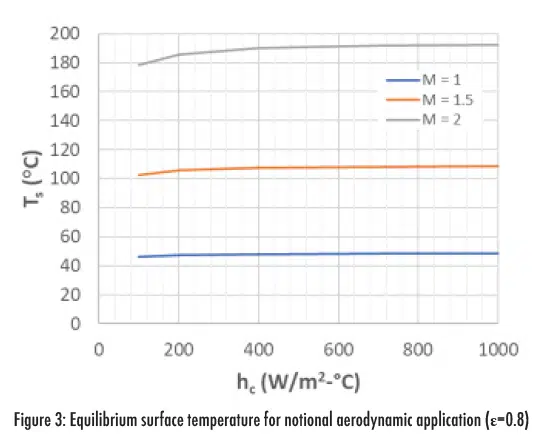
This equation can be numerically solved using any “goal seek” method, such as Solver in Excel, to identify the equilibrium temperature the body will reach. This is important to the field of electronics cooling because it sets the heat sink temperature for steady operation in these environments. An example is shown in Figure 3 for a few different Mach numbers in a 0°C environment. Note that the environment temperature will be a function of the altitude and location of operation. Similarly, the convective heat transfer coefficient will be a function of the altitude, body size, and body velocity. While this example illustrates the general themes only, the reader is referred to a detailed text, such as reference [4], for more information.
Overall, this example illustrates that radiation can also play a role in setting environmental operating temperatures in some extreme electronics environments. Given the high temperatures that can occur in these conditions, it may (i) justify development of robust electronics that can operate in elevated temperatures, or (ii) drive insulation requirements to ensure electronics aren’t damaged during transient exposures.
Space Applications
Lastly, we can’t talk about radiation without mentioning operation in vacuum conditions, such as satellites in space. In a vacuum there is no convection, and conduction is largely limited to heat transfer within the device itself. Thus, the primary means of heat transfer between a device and the environment is through radiation [2].
A basic steady-state heat balance is described in equation 13, where Qelx represents heat generation by the electronics, Qrad,in represents incoming radiation sources, and Qrad,out represents radiation to space. Incoming radiation sources include solar loading, albedo, and planet shine. Outgoing radiation is rejected to space, a heat sink at ~4K.
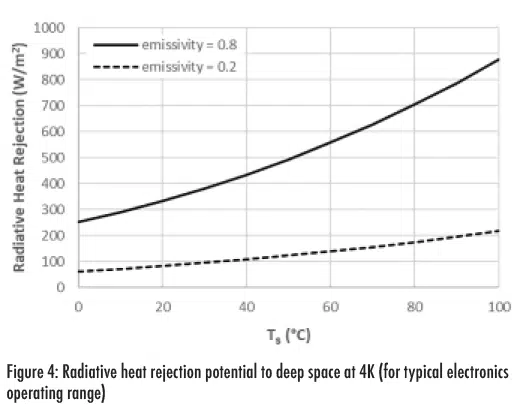
Figure 4 quantifies the range of heat flux rejected to space across typical electronics operating temperatures and emissivity values. These values are non-trivial and may rival that of solar loading in some cases (e.g. absorptivity values, orientations). In space applications, there may also be times where this heat rejection can cool electronics below their operating temperatures, requiring additional measures to be taken (e.g. heaters, insulation, orbit control, etc.).
The bottom line is that radiation matters in space environments, and the thermal engineer must consider both incoming and outgoing radiation sources.
Concluding Remarks
There is a common misconception that radiation only matters when temperatures are very high. This article challenges that assumption and provides several examples to help the practicing thermal engineer determine when they should account for radiation, or at the very least, when to double check their assumptions with early hand calculations. The following summary provides a starting point:
- Radiation is significant in natural convection environments and must be considered.
- Radiation is less significant in forced convection environment, but one should double check when velocities are low or geometrical dimensions are large.
- Radiation is the primary means of heat transfer in vacuum environments and must be considered.
References
[1] Frank Incropera and David DeWitt, Fundamentals of Heat and Mass Transfer, 4th Edition, Wiley (1996)
[2] NASA, State of the art of small spacecraft technology: thermal control, https://www.nasa.gov/smallsat-institute/sst-soa/thermal-control/
[3] Bruce Guenin, Don’t Underestimate Radiation in Electronics Cooling, https://www.electronics-cooling.com/2001/02/dont-underestimate-radiation-in-electronic-cooling/
[4] Robert Wesley Truitt, Fundamentals of Aerodynamic Heating, Ronald Press Company (1960)
[5] Ross Wilcoxon, A Simple Method for Estimating Radiation Heat Transfer, Electronics Cooling Magazine, Fall 2018