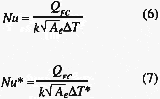Introduction
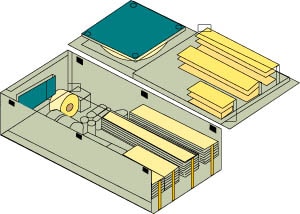
One of the more complex thermal problems in electronics is the modeling of complete systems, such as an enclosure containing electronic components. A typical example would be a power supply, including heat sinks and a cooling fan. This problem becomes more difficult when there are multiple heat sinks and other large components arranged in an arbitrary manner inside a box as shown in Fig.1.
Figure 1: General view of the electronics enclosure used for tests.
Steinberg [1] developed Eqs. (1 – 2), based on compiled data from Kays and London [2] for laminar forced convection inside a duct, in order to solve this type of problem:
| j = 2.7/ Re0.95HD , [Width(W)/Height(H)]=1 | (1) |
| j = 6.0/Re0.98HD , W/H <8 | (2) |
where the Colburn j-factor, and the Reynolds number, ReHD, are based on the hydraulic diameter, HD. Furthermore, Steinberg [1] recommended the correlation of McAdams [3] in the range of 104 < ReHD < 12 x 104:
| j = 0.023/Re 0.2HD | (3) |
Meanwhile, Mansingh [4] also recommended Eqs. (1 – 3) for this type of problem. It is very important to mention that the above equations were developed for the special case of duct flow. The solution obtained using Eqs. (1-3) is strongly influenced by hydraulic diameter, which is difficult to determine in this type of application.
In contrast, one can simulate this problem numerically using either finite volume or finite element techniques. However, it is neither convenient nor easy to obtain an accurate result, since most numerical simulations need a huge number of cells and several hours of computational time. It is also necessary to provide the numerical model with information on surface emissivity and view factors between the components and if this information is not available, it will decrease the accuracy of the numerical results.
The main objective of the present study is to conduct a series of experiments inside a complex electronics box in order to determine the forced convection heat transfer rate within the electronics box. This experimental data will be used to develop an empirical model that can be used as a design correlation.
Experimental Procedure
Figure 1 shows a complete view of the electronics box used in the present study. The dimensions of the box are 360 mm length, 170 mm width, and 95 mm height. The operating inlet velocity, V , range of the fan inside the box was 0.5 <V
< 1 m/s. The airflow at the entrance of the box was measured using a hot wire anemometer with a maximum error of 5%. The heat sinks were manufactured from 6060-T6 aluminum. The total effective surface area, Ae, of the test box, heat sinks and electronic components was estimated to be 0.437 m2 in the first and second setups, and 0.413 m2 for the third experimental setup. The power dissipation was varied within the range of 210 to 255 W.
The combined effect of free convection and heat radiation, QNC&R, was measured experimentally by operating the box at different power without the fan. The results were correlated as follows:
| QNC&R = 2.12 ( |
(4) |
where s is the average surface temperature and
is the arithmetic mean average of the inlet and outlet air temperatures. The steady state forced convection heat loss, QFC, from the electronics box was obtained as follows:
| QFC = QT – QNC&R – QW | (5) |
where QT is the total power expended towards the Joulean heating of the electronics box, QNC&R is the free convection and radiation losses and QW is the total conduction losses attributed to thermocouple wires and power leads. It was found that the free convection and the thermal radiation heat losses could contribute between 2% to 20% from the total dissipation heat. The present investigation considered that the free convection heat loss could be reduced linearly from the total heat losses based on the mixed convection model of Yovanovich and Vanoverbeke [5] for assisted flow. Also, Steinberger and Treybal [6] proposed a formula similar to Yovanovich and Vanoverbeke [5]; however, the thermocouple wire and power lead losses were neglected based on Refai-Ahmed et al [7]. They reported that the conduction losses, QW, for a sphere with a 60 mm diameter and dissipating power of 10 W in forced convection mode were in the order of 0.5% of the total input power.
The area-averaged Nusselt number is defined as follows:
where:
T = (Tsmax –
)
T* = (
s –
)
Tsmax = maximum surface temperature
The Reynolds number is also defined based on the effective surface area as follows:
where V is the inlet velocity to the enclosure. The thermal conductivity of the fluid, k, is evaluated at the film temperature.
Both the Nusselt and Reynolds numbers are defined based on the scale length of and the overall uncertainties for both of them are ±5% and ±3% respectively.
Most of the experimental tests were performed at an ambient temperature of 298 K. However, three tests were performed inside an environmental chamber at an ambient temperature of 333K. For these tests, the electronic enclosure was isolated from the surroundings but the inlet and outlet remained open to allow for unrestricted air flow. This arrangement should minimize the effect of the circulating air inside the chamber.
The experimental series was conducted in three different setups. The first and second setups have the same total surface area, Ae = 0.437 m2. The first setup had the electric loads equally distributed along the heat sinks; however, the second setup had the electric loads in the front of the heat sinks, as shown in Fig. 2. The third setup has a surface area of 0.413 m2. The surface area was reduced due to cutting away a part of the heat sink’s base. As a result, the electric loads in this case were shifted to the rear section of the cut heat sinks, as shown in Fig. 2.
Figure 2: Electric load distribution along the heat sinks.
Experimental Results and Discussion
An important issue in a study dealing with different body shapes is the presentation of the relationship between the Nusselt and Reynolds numbers. The present scale length was proposed by Yovanovich [8] and was examined by both Jafarpur [9] and Refa Refai-Ahmed and Yovanovich [10] in free and forced convection modes, respectively. The present study found that
is the most appropriate scale length, where it is possible to calculate and measure by comparing to the hydraulic diameter.
Figure 3 shows the relationship of Nusselt and Reynolds numbers, which are based on the scale length of .
Figure 3: Relationship of Nusselt and Reynolds Numbers based on maximum surface temperature (Pr = 0.71)
The experimental results of setups 1, 2 and 3 can be correlated as follows:
| Nu = mRen | (9) |
The constants m and n for the different setups are given in Table 1.
| Setup | A e , m2 | m | n |
| 1 & 2 | 0.437 | 0.041 | 0.853 |
| 3 | 0.413 | 0.125 | 0.731 |
Table 1. Numerical values of constants in Eq. (9) for different setups
Figure 3 also reveals that the experimental data of setups 1 and 2 follow one common slope. However, the experimental results of setup 3 were below the data of setups 1 and 2 by approximately 12%. Figure 4 shows the relationship between Nu* and Re for the present data, where the Nusselt number was defined based on the average surface temperature. One can observe that the experimental data was shifted upwards. The experimental data was also correlated in the following form:
| Nu* = m1 Ren1 | (10) |
The constants m1 and n1are given in Table 2.
| Setup | Ae, m2 | m1 | n1 |
| 1 & 2 | 0.437 | 0.07 | 0.855 |
| 3 | 0.413 | 0.023 | 0.845 |
Table 2: Numerical Values of Constants in Eq. (10) for Different Setups
Both Fig. 3 and Eq. (9) reveal that the Nusselt number is a function of the effective surface area and Reynolds number. Therefore, it is expected that Nu will decrease with reducing surface area until approaching the result for a rectangular duct, having a surface area A0, where A0 = 0.191 m2 in the present study. In addition, McAdams [3] and Sieder and Tate [11] found that Nusselt number was proportional to Prandtl number, (Nu Pr1/3) for Pr > 1. In the present study the constant m has a functional dependence on Pr1/3 and the area ratio of effective surface area to a bare duct, Ae / A0. Therefore, Eq. (9) can be presented as follows:
| Nu = 0.03 [Ae/A0] Re0.8 Pr1/3 , | (11) |
104 < Re < 105, 1 < [Ae/A0] <2.3
where
m = 0.033 [Ae/A0] Pr1/3,
n = 0.8
The maximum and average differences between the proposed model Eq. (11) and the present data are 10% and 6.3%, respectively. Equation (11) is also consistent with McAdams [3] correlation, Eq. (3). For comparison purposes, Eq. (3) is represented based on the scale length of , as shown in Eq. (12) and the ratio of the pipe length to the diameter was assumed to be 50.
| Nu = 0.038 Re0.8 Pr1/3, | (12) | |
| 104 < Re <15 x 105 , Ae/A0 = 1 |
It was found that the difference between the present model, Eq. (11) and McAdams [3] is around 13%.
While Eq. (11) was developed based on empirical testing for a specific case study, the model can be applied to other cases such as forced convection inside a pipe and can predict the Nusselt number within 13%, as previously mentioned. Steinberg [1] recommends the use of the McAdams correlation for electronic applications that have internal forced convection. However, the McAdams correlation is strongly influenced by the hydraulic diameter, which is difficult to determine and therefore Eq. (11) is recommended in these types of applications where good accuracy is required.
Figure 4. Relationship of Nusselt and Reynolds Numbers based on average surface temperature (Pr = 0.71)
Finally, the experimental data in Fig. 4 can be modeled, similarly as Eq. (9), as follows:
| Nu* = 0.033 [Tsmax – |
||
| 104 <Re < 105 , 1 < Ae/A0 < 2.3 | (13) |
where
m1 = 0.033 [Tsmax – /
s –
] [Ae/A0] Pr1/3
n1 = 0.8
This simply means that:
| Nu* = Nu [Tsmax – |
(14) |
Summary and Conclusions
The present study conducted a series of experiments inside an electronics box. The experimental data were used to develop a general experimental model, Eq. (11). This model can be used to predict both the maximum and average temperatures inside a closed electronics box, within the range of 104 < Re <105 and 1 < Ae/A0 < 2.3. It is also in close agreement with the earlier correlation of McAdams [3] by 13%, and 6.3% with the present data.
References
| 1. | Steinberg, D. S., 1980, Cooling Techniques for Electronic Equipment, John Wiley & Sons, New York. |
| 2. | Kays, W. M. and London, A. L., 1964, Compact Heat Exchangers, McGraw-Hill, New York. |
| 3. | McAdams, W. H., 1954, Heat Transmission, McGraw-Hill, New York. |
| 4. | Mansingh, V., 1995, “Practical Electronics Cooling: Analysis, Modeling & Measurements”, Short Course Notes Presented at IEPS Conference, Atlanta. |
| 5. | Yovanovich, M. M. and Vanoverbeke, C. A., 1988, “Combined Natural and Forced Convection Heat Transfer from Isothermal Spheres”, AIAA-88-2618, AIAA Thermophysics, Plasmadynamics and Laser Conference. |
| 6. | Steinberger, L. and Treybal, R., 1960, “Mass Transfer from a Solid Sphere to a Flowing Liquid Stream”, AIChE Journal, Vol. 6, No. 2, pp. 227 – 232. |
| 7. | Refai-Ahmed, G., Yovanovich, M. M. and R. Culham, 1997, “Experimental and Approximate Analytical Study of Forced Convection with the Effect of Turbulence Intensity from Isothermal Spheres”, J. Thermophysics and Heat Transfer, Vol. 11, pp. 223-231. |
| 8. | Yovanovich, M. M., 1987, “New Nusselt and Sherwood Numbers for Arbitrary Isopotential Bodies at Near Zero Peclet and Rayleigh Numbers”, AIAA-87-1643, AIAA 22nd Thermophysics Conference. |
| 9. | Jafarpur, K., 1992, “Analytical and Experimental Study of Laminar Free Convection Heat Transfer from Isothermal Convex Bodies of Arbitrary Shapes”, Ph.D. Thesis, Mechanical Engineering Department, University of Waterloo, Waterloo, Ontario, Canada. |
| 10. | Refai-Ahmed, G. and Yovanovich, M. M., 1997,” Experimental Study of Forced Convection from Isothermal Circular and Square Cylinders and Toroids”, J. Heat Transfer, Vol. 119, pp. 70-88. |
| 11. | Sieder, E. N. and Tate, G. E., 1936, “Heat Transfer and Pressure Drop of Liquids in Tubes”, Ind. Eng. Chem., Vol. 28, pp. 1429 – 1436. |