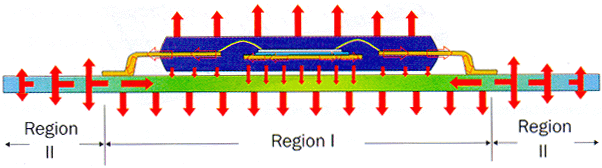
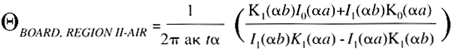In last issue’s column, a method for calculating the thermal conductivity of a printed circuit board (PCB) was described. Now, we look at a more complicated heat transfer process, namely the loss of heat from the surface of a PCB to the ambient air. This situation is more challenging to describe mathematically since it involves the simultaneous processes of heat spreading by conduction and heat extraction over the surface of the board by convection and radiation. The figure below illustrates the heat flow patterns for a leadframe package attached to a test PCB. The efficiency of heat transfer from the PCB to air has a significant effect on the temperature difference between the chip and the air.
Figure 1. Heat flow patterns for a leadframe package attached to a test PCB
In this simple representation of the PCB, the temperature of the board is considered as constant within the region bounded by the package footprint, or Region I. Beyond the footprint, in Region II, the temperature decreases in an exponential fashion. The thermal resistance to air of Region I is calculated from the expression
where h is the heat transfer coefficient and A is the area of Region I. The thermal resistance to air of Region II is calculated from the circular fin formula
where = (2h/
t)0.5 and I0 I1 (K0, K1) are modified Bessel functions of the 1st (2nd) kind, order 0 and 1,
is the thermal conductivity of the PCB and t is its thickness. a and b are each the radius of a circle with the same area as the package footprint and the PCB, respectively. While this formula may appear intimidating, Bessel functions are available in popular spreadsheet software programs.
BOARD-AIR is calculated from these two resistances, considering them to be a parallel resistance network.
As an example, consider a typical JEDEC-standard test PCB, having a thickness of 1.59 mm, two, 36 µm thick, internal planes of copper, and surface traces with an area-averaged thickness of 14µm. The graph in last issue’s column provides a value of in-plane conductivity of approximately 20 W/m-K. The effect of air velocity on h can be determined by referring to this column in the January 1998 issue. At forced air velocities of 0, 1.0, and 2.5 m/s, h will have the approximate values of 15, 30, and 45 W/m2-K.
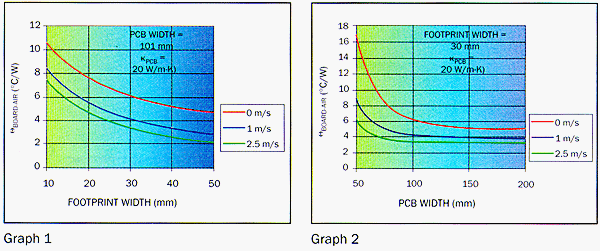
The two graphs below indicate the relationship between BOARD-AIR and the width of the package footprint (graph 1), and the PCB size (graph 2), at the three air velocities considered.
The first graph shows that increasing the size of the package thermal footprint produces a significant reduction in BOARD-AIR. This is due to the increased size of Region I of the PCB, which transmits the heat to the air with minimal spreading resistance losses. One should note that in applying this graph to BGA packages, the thermal footprint width will normally be less than the actual width of the package, leading to a higher
BOARD-AIR than for a similarly sized leadframe package.
The second graph shows that, for the specified value of PCB, once the width of the PCB exceeds 100mm, further increases in the size of the PCB produce diminished reductions in
BOARD-AIR. This trend is exacerbated with increased air velocity.